Qualitative Complexity
Pavel B. Ivanov
Troitsk Institute for Innovation and Fusion Research (TRINITI)
E-mail: unism@narod.ru
Written: 2 December 1996
Revised: 1 April 1997
|
Abstract
Different attitudes to the problem of complexity evaluation
are categorized within a general scheme representing the levels
of integrity. Complexity becomes distinguished from singularity
and unity, and implies three distinct types: multiplicity,
coherence and order. Structure, system and hierarchy are
described as the levels of coherence, and the respective
measures of complexity are discussed. The principles of
the hierarchical approach are formulated, and its relations
|
Introduction
Contemporary science has come to a clear understanding of the
necessity of studying the development of any object to comprehend
its structure and behavior [1]. The first intuitive
idea of an object's development associates it with the growth of the
object's complexity, and the existence of different levels within
the object. The consideration of hierarchical structures and
hierarchical systems [2] leads to the natural
question: "What is the multilevel organization as such, and where
it comes from?" In particular, such investigation might bring
light to the problem of the distinction of structural and
systemic description, which often get mixed in the literature
[3]. One more goal that might be achieved in such a
study is the reconstruction of the object's integrity and discovering
the directions of its development, rather than focusing on arbitrary
details and the peculiarities of behavior [1].
The recent interest to the study of complex systems poses, along
with the numerous technical issues, many fundamental questions.
What is the organization of a system? How "complex"
systems differ from "simple" ones? What should be meant
under the "small", "large" and "superlarge"
system? Thus, the sense of complexity may differ at different
levels and for different objects — and it would be desirable
to have some qualitative distinctions before trying to construct
any formal measures of complexity. Indeed, there are many such
quantitative measures [4,5], and it is not always
clear what they actually evaluate.
In many cases the answers are sought in hierarchical considerations.
The literature is replete with different hierarchical constructions,
and some authors suggest distinguishing the hierarchy (development) as
a separate level of complexity, along with the structure (static level)
and the system (dynamic level) [1]. It is well known
that hierarchical organization may be the key to efficient control
in large systems [6]. Yet another hint comes from
nonlinear physics, considering strongly non-equilibrium systems with
their own order. It has been found that the behavior of such systems
may be dependent on the sequence of catastrophes they have passed
to the moment of observation, and hence the history of the system would be
represented in its current state [1][7].
Development and hierarchical organization were thus related to
nonlinearity, self-action.
Analogous phenomena have been known in philosophy since long ago,
under the name of reflection, which, however, was mostly
associated with subjectivity. The recognition of the
different forms of reflection might lead to a better understanding of
the differences between the physical, organic and subjective levels
of development. This would be one more step to the integrity of
science, which has been earlier sought within structural and systemic
approach [8].
Levels of integrity
Each science is dealing with its specific object, and any consideration
has to start from the fundamental concepts which cannot be introduced
within the science and should be borrowed from somewhere else,
representing the first intuitive view of the field. On the other side,
these a priori concepts outline the scope of relevant problems
and delimit the range of applicability. For studying complexity, the
notion of integrity might be taken for such a starting point.
Thus, to speak about complexity of something, one must first
insure that this "something" may be considered as an
entity distinguished enough from the rest of the world. That is,
the natural premise to complexity studies is the existence of
integral "wholes" whose complexity could be further
described. This means that complexity may only be defined in
respect to that integrity, being one aspect, or one form of it.
The first, most primitive form of integrity is singularity.
At this level, the object is considered as unique and isolated,
without any regard for other objects. No internal organization
or external relations are considered, and therefore the object
is quite simple. The only definiteness it may possess is
its very existence. Not much can be inferred from such a primitive
consideration — still, this is the necessary first stage of any
study, the recognition of the problem.
On the next level, the simplicity of this recognition gives place
to the observation of external dependencies and internal
inhomogeneity — this is where one can speak about
complexity. The object is considered together with its
environment, and the object's interaction with it leads to
specific structures, processes or kinds of development. The object is no
longer unique and simple, being rich enough to be studied by
various sciences, from their specific points of view. The
integrity of the object may therefore seem violated, being
potential rather than actual, and a "metascientific"
approach is required to provide a unified view.
The level of unity restores the singularity of the object
retaining its complexity. The object becomes completely reflected
in its environment, while this environment is completely
represented "inside" the object. The features of the
object are just the traces of its history, and its behavior is
non-local, being controlled by the higher-level development.
However, this level escapes purely scientific consideration,
being essentially influenced by practice.
Now, when the level of complexity has been related to the
other levels of integrity, one can proceed with unfolding
the hierarchy, distinguishing different types of complexity itself.
Its definition as a path from singularity to unity provides a
logical basis for such a distinction. Thus, one can conclude that
there are two sides of complexity reflecting its relation to these
extremes, and that there should be an intermediate level linking
them into a hierarchical whole.
The level of complexity extending singularity in a minimal way
is multiplicity. There are many instances of the same
singularity, as if produced by some cloning procedure, when each
clone remains simple and isolated from the others,
but not unique this time: there are many such objects,
defining a specific object class by the very fact of their
existence. Still, the objects of the same class enter no
interrelations beyond the simple equivalence, mere belonging to
the same class. Any one of them could be chosen as a
representative of that class, and the whole class can be
restored from every single element. Therefore, the complexity
of such class may be related to the number of its elements, and
the hierarchy of multiplicity coincides with the hierarchy of
cardinal numbers.
The unity side of complexity might be called order,
including both the sense of "being properly made,
arranged", and the sense of "as it should be".
In a sense, this is the "most complex" complexity,
since it cannot be comprehended in the purely objective terms,
being unfolded into a "teleological" hierarchy.
Historically, the difference between multiplicity and order
is the ancient opposition of Chaos and Cosmos — the
opposition that gave birth to all the earthly things. This
earthly way from Chaos (multiplicity) to Cosmos (order) is
the intermediate level of complexity introducing some
congruencies into the chaotic multiplicity, while leaving
enough space for extensive and intensive development of the
local order. This kind of complexity might be called
coherence.
So, multiplicity is associated with disorder, coherence means
partial order, while on the highest level order becomes
complete, universal.
Moving deeper into the hierarchy of complexity, one could use
the same logical scheme, distinguishing the opposite aspects
of coherence joined by an intermediate level. This procedure
leads to the three levels of coherence: structure, system and
hierarchy.
The first category of this triad, structure, refers to
internal coherence, representing the object as a collection
of elements and their links. This representation is least
different from multiplicity, the only new feature being the
division of the multiplicity into two classes, one called
"elements" and the other called "links".
Being the internal characteristic of the object, structure
may be thought of as the static aspect of the object.
The inverse of structure is system, the second level
of coherence. It refers primarily to the external manifestations
of the object, the way it "moves" in its outer space,
altering its relations with the environment. Since these
relations are somehow structured, system may be generally
considered as the way of transforming one structure into
another. So, the basic category at the systemic level is
"transformation", or "transition" —
and therefore system represents the object's dynamics.
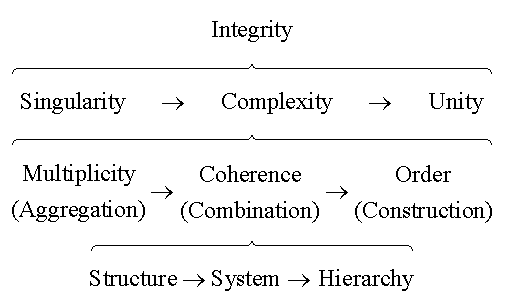
Figure 1. The hierarchy of integrity.
Logically, the next level of coherence should be the synthesis
of the internal description provided by structure and the
external systemic treatment. It should consider the object
both statically and dynamically, so that systemic
transformations lead to the internal changes in the object,
which nevertheless retains some of its structural features as
to remain the same in these transformations. This is
the level of development — and the synthesis of
structural and systemic features is hierarchy.
Thus, complexity itself becomes complex, comprising the
hierarchy of possible forms (Fig. 1).
One level of distinction provides the triad of multiplicity,
coherence and order — on another level, one might
distinguish structural complexity, systemic (functional)
complexity, and hierarchical (developmental) complexity.
Incidentally, this sequence reflects the history of
methodological thought in the XX century: the beginning
of the century was marked by the structural approach, which
gave way to systemic approach in the middle of the century,
while the end of the XX century passed under the dominance
of the idea of development, which receives its formal
expression in the hierarchical approach.
Structure
The most general idea of structure is linking some relatively
distinct elements by a number of links. Typically, structure
is modeled with a set and relations on it: the elements of
the set represent the elements of the structure, while the
links are associated with the n-tuples of the elements
belonging to an n-place relation. However, the links
may be treated as independent entities, like arrows in the
categorial approach [9]; in this case, one needs
to explicitly define the beginning and the end of each arrow.
The support set may be either discrete, or continuous, or
even more powerful. Accordingly, the relations may vary from
the finite number of element pairs to connectivities on a
non-trivial manifold. Links may be either rigid, or stochastic,
or any combination of the two. All these possibilities fall
under the scope of traditional mathematics, which may be
called the science about structures, in general. Since
structure refers to the static side of the whole, it becomes
clear that mathematics is incompatible with any motion, and
this explains why mathematicians made their best to expel
movement (and development) from mathematical language, and
even the modernistic mathematical trends (like constructivism)
speak of dynamics in a static way, imposed by the traditional
forms of mathematical reasoning. That is, the mathematical
description of a process refers to the structure of the
process only; accordingly, mathematical models of
development mainly reflect its structural aspect
[comment].
The simplest structure [comment].
is given by a finite set
S = {si: i=1,...,N}
with a single two-place relation
L: S®S
defined on it. When a pair <si,
sk> belongs to relation
L, one says that element
si is linked to element sk
by the link
lik Î L.
Such link is oriented, and
lik ¹ lki;
moreover, relation L need not contain
both lik and
lki, so that if one element
is linked to another it does not imply that there must be a link
back. Denoting the set of the elements of S which are
linked to some other elements with dom(S) and the set
of the elements that appear in the right-side of the pairs
from L with rng(S), one can
observe that, in general,
dom(S) ¹ rng(S),
dom(S) ¹ S and
rng(S) ¹ S.
In the trivial case,
L is empty, and the structure reduces
to mere multiplicity. At the opposite extreme, any element is
directly linked to any other, and
L = S2.
However, structure is more than just elements and links —
it is a kind of wholeness, a level in the hierarchy of integrity
[comment].
In the above model, the appearance of this integrity might be
described as follows.
The direct links between the elements of S represented
by l Î L are not the only connections between them.
Thus, the relation L may contain both
pairs lik and
lkm, which means that there
is a mediated link between si and
sm (Fig.2a) — and this
does not depend on whether there is the direct link
lim or not. Longer chains
may be constructed as well, and one comes to considering the
hierarchy of indirect links which is one more
manifestation of the same structure.
Yet another structural feature is the formation of
collateral links. For example, if both
lik and
lmk belong to relation
L, elements si and
sm are naturally related to each other as the
predecessors of the same element (Fig.2b).
Similarly, if both
lki Î L
and lkm Î L
then there is a collateral link between si and
sm , which have a common predecessor
(Fig. 2c).
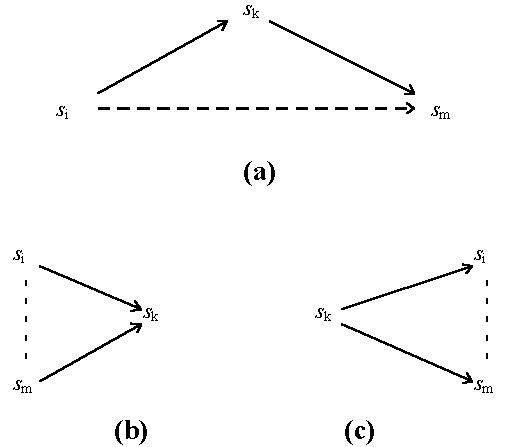
Figure 2. Indirect links: (a) mediated; (b,c) collateral.
Direct, mediated and collateral links may be combined in various
ways, the numerous kinds of indirect links thus obtained
being the manifestations of the same structure. If an element
s Î S
participates in at least one pair l Î L,
it becomes, in one way or another, connected with any other such
element. The elements which are not linked to any other element
(or to themselves) by L are completely
irrelevant to the structure, so that the set dom(S) Ç rng(S) can
be considered as the set of the structure's elements in the
applications, instead of S. Note the difference between
irrelevant and isolated elements: the former
merely do not belong to the structure, while the latter are just
linked to themselves only, with no direct or indirect link to any
other element.
The distinction between elements and links within the structure
may be relative. Thus, if element sk mediates
the link between elements si and
sm, it may be considered as a higher-level link
connecting lik and
lkm. Since any two elements
of the structure (discarding the irrelevant elements) are somehow
connected, any element can thus become a link between links,
so that the links will play the role of the structure's elements.
Hence, any particular subdivision of the structure into elements
and links does not follow from its own properties, but rather
from some conditions external to the structural approach proper.
When a number of "primary" elements and links are
selected, the rest of the structure can be accordingly unfolded;
for another choice, the structure will unfold differently.
Such refoldability makes the structure hierarchical.
The existence of different unfoldings, with the respective
levels of integrity, means that there is no universal quantitative
measure of structural complexity. Moreover, even though
one might evaluate structural complexity for every particular
unfolding, there may be a hierarchy of different measures, not
always reducible to a single number. Thus, in the simple
relational model described above, one might count the total
number of links and divide it by N2 (the
maximum possible) to obtain a kind of probability (frequency)
p. Then, a global measure of structural complexity
could be introduced as
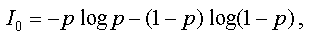
which is the well-known formula for the quantity of information.
The value I0 is equal to zero when there
are no relevant elements in the structure, or for a maximally
connected structure, when
L = S2.
This agrees with the intuitive idea of structural complexity:
the structures without links are quite simple, as well as the
"rigid" structures with the elements linked in a
"completely deterministic" way.
An alternative approach is to count the number of
"arrows" beginning at a given element
sk and divide it by N to obtain the
normalized values pk lying in [0,1].
Evidently,
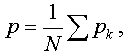
so that the "probability" p introduced via
counting links is just the average "probability"
of an element being linked to the structure. Since all the
pk are mutually independent, one could
evaluate the information contained in the set
{pk} as
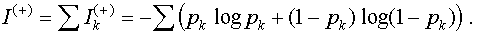
Analogously, one could define the value
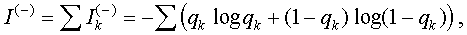
where qk are the counts of arrows with the
end at the element sk divided by N.
Though, evidently, the average frequency p may be
expressed through qk too as
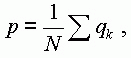
the quantities I(+) and
I(-)
do not coincide, and the measure I0 becomes
split into two dual measures I(+) and
I(-).
Of course, the process can be continued, to account for indirect
links and substructures. For example, every two elements
si and sk may be assigned
with a numerical weight cik indicating the
"level of connectedness" of these elements within
a given unfolding of the structure. The weights
cik can be chosen from the interval [0,1] so
that cik = 1 if the two elements are connected
in every possible (direct or indirect) way, while
cik = 0 would mean that there is no connection
between the elements, that is, the structure splits into mutually
isolated substructures. Then, a gross measure of complexity can
be introduced as
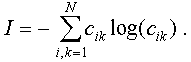
The set of weights {cik} may be
considered as a fuzzy subset of S2
[10,11]. In general, cik
cannot be interpreted as probabilities, since they do not
necessarily satisfy the "normalization conditions",
as specified in [11]. However, there may be
classes of valuation functions that can be associated with
cumulative probability distributions [12];
the complexity measure I will become a kind of entropy
in this case.
I should stress that structure as a level of coherence does not
imply any restrictions on the type of elements and links. Thus,
there may be "material" structures, with both elements
and links of a material nature; however, there may also be
completely "ideal" structures, or some mixtures of the two.
System
A typical abstraction of system might be represented by a
collection of triads
{<Sin, Sc, Sout>},
where Sin and Sout are the
input and output structures respectively, while Sc
denotes the current state of the system, often identified with
its "internal" structure. Depending on the level of
consideration, each of these three structures may be differently
unfolded, providing the special models known in the literature.
Thus, the completely folded Sc leads to the
notion of "black box", which evidently correlates with
the idea of elementary operation in the theory of computability
[4], or with the basic arrows in the categorial
approach [9]. In a more unfolded form,
Sc may be any composition of such elementary
operations, implementing an algorithm of "calculating"
the output structure by the input structure, the "white
box" [13]. Complexity on the systemic level
may therefore be called algorithmic, or
computational complexity [4].
One might develop a simple model of system analogous to the
relational model of structure described in the previous section.
Thus, Sin and Sout might be
chosen from the same class of structures representing the states
of the system's environment; then they will be analogous
to the elements of the structure, while operators Sc
connecting them will be the analogs of structural
links l. The only difference is that
the "elements" connected by such functional link are
external to the system, unlike internal elements of the
structure. This is the characteristic duality of any system:
on one side, it functions like a structured object — while
on the other side it can be considered as just a more detailed
specification of a structural link.
The formation of mediated links finds its systemic-level analog
in the external composition of systems, when the initial
state Si of the environment is transformed
into the final state Sf via an intermediate
state S*:
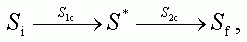
which may be considered as the construction of a new operator
Sc = S2c°S1c.
Like with structures, such sequential
compositions (or cascades) can form long chains; since
an elementary systemic transformation (operation) may be thought
of as a transition, the composite functions represent
processes. For example, the movement of a point
x in a configuration space X can
be considered as sequential transformation of structures:
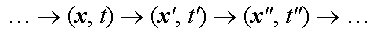
In this case, the operators transforming one structure into
another must be associated with the respective elements of the
tangent space TX, velocities. Such an approach is
typical for classical physics, and especially classical mechanics.
The other kind of indirect links, collateral links, can be
associated with the parallel composition of systems, when
several input or output structures are united into a joint
input/output. This means that a class of structures
would serve as the system's input or output, instead of a
single structure; along with the basic structures, such class
would include all the possible sets composed of the basic
structures. For example, a binary input is a single-element
structure s ; when two such structures s and
s' are composed into a parallel input, there may be
combinations (s), (s') and (s,s')
as the possible values of the same input. In a more complex
case, one could consider some distributions of elementary
inputs as the "microscopic" realizations of a
"macroscopic" variable. Such parallel composition
of systems is widely employed in statistical physics. Various
combinations of sequential and parallel composition may be found,
for instance, in quantum theory.
The external nature of systemic coherence leads to a kind of
integrity quite different from the internal integrity of the
structure. The system's integrity has to be comprehended from all
the variety of its relations with the environment, rather than
from the internal structure of the system. Generally,
functional complexity is revealed dynamically, in the process
of functioning [14]. Consequently, it cannot
be described in a static way, and this is the main source of
any problems with "computability", leading to the
numerous forms of the famous Göedel theorem
[15] [comment].
Systemic complexity is complexity of functioning, and it should
not necessarily correlate with the complexity of the structures
involved. Functional complexity is the property of a single
element, or a structure as a whole, rather than of the way the
elements are connected, and, in this sense, it is
complementary to structural complexity [16].
For example, a computer program may be very long —
but all it does is a constant output; a nail may be driven in
either with a hammer, or using a complex cybernetic device, etc.
However, the complexity of the "white boxes" modeling
a system would generally correlate with functional complexity
if these models are built of some "standard" elements,
whose functional complexity does not change when they are
connected into a system. In the simplest case, the
external model of a system ("white box") may
be constructed of the elements of unit complexity — and
then the algorithmic complexity of the composite system
would be represented by the complexity of the junctions. Such
systems are completely "transparent", though they do
not have to be deterministic.
Still, there is a difference between the system and its model
of the "white box" type. Since the goal of such
modeling is to reconstruct functioning only, the model may
be built of the blocks different from the "matter" of
the original system — and this would allow a partial
reconstruction of behavior only, with some properties of the original
system discarded. That is, the original system is modeled on
a definite level — and the variety of such models is the
systemic counterpart for the various unfoldings of the structure.
Usually, all the lower-level functioning is considered as
side effect, so that different systems model each other
to that accuracy. However, there is also an analog of the
structure's refoldability: the properties that are considered
as side effect in one situation, may be essential in another.
Like the distinction of elements and links of the structure may
be relative, there is a mutability of subsystems and their
junctions. Thus, for the sequential composition of two functional
blocks described above, the triad
<S1c, S*, S2c>
may be considered as a component of a system, so that the
intermediate structure S* will play the role
of the internal structure of this system, rather than the state
of environment. In the operator S2c°S1c,
the junction °
(represented by the structure S*) transforms
the output of S1c into the input of S2c.
As in the case of structures, systems may be either material,
or ideal, or of a mixed type. The definitions of this section
remain applicable in each case — though the functional
treatment of the system might be not evident sometimes. Thus,
systematization often means mere classification, which seems
to be closer to the structural level. However, taxonomy can
be a system if it is used for categorization, implementing the
transition from the appearance of the object to its essence, and
then to its more subtle features. Still, there is no rigid
boundary between the structural and systemic levels, and they
usually become intricately interwoven in practice, representing
the two sides of the object's hierarchy.
Hierarchy
Though hierarchical approach may be considered as a logical
completion of the historical line from the structural methodology
to the system paradigm, the notion of hierarchy is much older,
ascending to the mythological cosmology of the primitive societies.
The first manifestation of hierarchy is the presence of several
qualitatively different levels with a kind of vertical order,
when one level may dominate over another, so that the relations
between the levels are of a kind other than the relations inside
each level. Up to the recent time, the origin of this order was
unknown — and hence hierarchy seemed to be imposed by some supreme
force, which is reflected in the very word "hierarchy":
"the sacred order". Now, it is clear that the levels
of hierarchy represent the stages of its history, and that
reflection (nonlinearity) is the key to any development
[1].
Most generally, reflection is the interaction of the object with
itself, which implies self-relation and self-transformation. At
the structural level, reflection can be represented by linking an
element of the structure to itself; in particular, the reflexivity
of a relation l Î L
means that <s, s> Î L
for any element s Î S.
However, this is not the only way to introduce reflection into
the structural description, since an element of the structure may
be linked to itself indirectly, via mediated or collateral links.
The depth of indirection may be a criterion for the distinction
of the different levels of the structure, when it is unfolded starting
from a fixed element. Of course, the same structure may be unfolded
in many such hierarchical structures.
For the system, reflection is easily associated with a cyclic process,
when the system's output may change its environment, which would affect
the system's input, and so on; this is the common feed-back scheme.
When the part of environment that provides such feed-back is included
into the system, the system acquires at least two levels, one of which
corresponds to the "pure" functioning, while the other
accounts for "self-regulation", like in the usual operation
analysis [13,ch.4]. The system thus becomes
hierarchical.
Since any hierarchy can only manifest itself through the variety of
its hierarchical structures and systems, there may often be a lack of
awareness of the hierarchy itself. The different structural and
systemic description then seem uncorrelated and even controversial,
and there may be hot argument between their adepts, claiming their
own attitude the only truth. However, these contradictions are most
likely to be merely apparent, being the aspects of the integral
description [17].
The basic features of hierarchy might be summarized as follows:
-
Hierarchy can be unfolded into numerous hierarchical structures, and
its external behavior is, at any instance, that of a hierarchical
system.
-
There are no rigid levels of hierarchy, but rather hierarchy is
characterized by infinite divisibility. Thus, the relations between
any two levels of hierarchy constitute a specific entity which may
be considered as a level of the same hierarchy lying between
the two original levels. Therefore, there is no "complete"
structure of the hierarchy, since one can always find a new level
between any two previously discovered.
-
The collection of intermediate levels between any two levels of
hierarchy may be folded into their direct connection, so that
the total number of levels would be diminished. The different ways
of folding and unfolding the hierarchy lead to its various
manifestations, or refoldings.
-
Because of refoldability, there is no absolute "topmost level"
in the hierarchy, though any hierarchical structure would possess one.
Any element of hierarchy may become its top unit, thus representing
the hierarchy as a whole.
-
Hierarchy is not a simple ordering of levels, but rather a
multidimensional formation. The number of its dimensions is as
infinite, as the number of levels. However, each unfolding implies
a one-dimensional ordering of levels, and the levels may be
characterized by a definite dimension.
-
Within hierarchy, the distinction between the elements and their
connections may only refer to a single unfolding, thus being
relative. In the same way, any functional decomposition is related
to a definite hierarchical system, based on the respective unfolding
of the hierarchy.
-
There is a kind of self-conformity in the hierarchy. Any component
of hierarchy is a hierarchy too, and it may be unfolded in the same
way as the whole hierarchy. The very distinction between the part
and the whole becomes relative, since every single element of
hierarchy reflects it all, contains it within, thus being equivalent
to it.
The "own" hierarchy of any object is another side of the
hierarchy of its environment. Reflexive interaction with the
environment leads to the object's development. Since refoldability
assumes many ways of interfacing the external world, development
may follow different routes, and different unfoldings of a hierarchy
indicate the possible ways of its development. Being the unity of
the internal and the external, hierarchy assumes two directions of
development: it may either "zoom in" unfolding its
elements and their connections — or it may grow through joining
several hierarchies in one. These acts of integration and
differentiation change the organization of hierarchy.
Like with the indirect links in the structure, or the processes at
the systemic level, the interactions of the objects in the world may
be mediated by other objects, up to the most distant influences.
The integrity hence arising unites the objects with their environment,
making the whole world a unity. However, this unity should be
treated hierarchically, and it cannot be comprehended as a given
entity, or a process — again, it is a synthesis of the both.
The object's interaction with the world may be represented by the
cycle of alternating phases (levels) of action and being acted upon.
The object is reproduced in each cycle, though in another
state. The simplest case of such reproduction is hierarchical
refolding, leaving the object the same and merely changing its
"form", or its "position" in the world. One
more possibility is extensive reproduction, or expansion,
when a larger part of the world becomes involved in the object's
environment, while the character of interaction remains generally
unchanged. The next level is intensive reproduction, or
development proper, which implies a shift of the boundary between
the object and its surroundings, the change in the very notion of the
internal. Evidently, this means a synthesis with some other hierarchy,
formerly attributed to the external world.
One cycle of the object's self-reproduction provides a natural measure
of time, associated with this particular development. Such
time should be considered as hierarchy, since the cycle of reproduction
looks differently at different levels of hierarchy, thus defining
different time "scales". It differs from the time variable
known in physical sciences, where it is a structural parameter rather
than a measure of the level of development, hierarchical
complexity. The hierarchical notion of time reflects its intuitive
features, such as directedness from the past to the future, the
existence of a finite "now" within each reflection cycle,
and the difference in the "natural" time flow for the
objects of different type.
Conclusions
The hierarchy of integrity discussed in this paper may be unfolded
in different ways. One of them has lead to the hierarchical
understanding of complexity, which could become a framework for
further qualitative and quantitative specifications. Like structure,
or system, the category of hierarchy is universal, so that
any object can be treated hierarchically. All the hierarchies are
identical in their organization, and may be considered the unfoldings
of the same hierarchy, the different sides of the same world. This
may pose many delicate questions concerning the correspondence
between natural or artificial hierarchies. Thus, ideal links may
become quite material bonds, directedness of development may assume
the form of purposefulness, the abstractions of scientific analysis
and synthesis may transform into practical development as destruction
and reconstruction. One could further unfold the hierarchy of
complexity, to cover the categories like "collection",
"arrangement", "compound" or "mixture".
Another direction of unfolding leads to such characteristics as
"balance", "stationarity", "stability",
"robustness" etc. One of the most important areas of
hierarchical study is the investigation of different levels of
mediation: passive, random mediation is typical for the inorganic
world, while the organic level is characterized by active, or
forced mediation, and the level of subjectivity is marked by the
universal and arbitrary mediation, when any two objects become
interrelated due to the projection of the world into the mind.
[comment]
References
- E. N. Yeliseyev (1983), The structure of the development of complex
systems (Leningrad: Nauka)
-
M. D. Mesarovic, D. Macko, and Y. Takahara (1970), Theory of
hierarchical multilevel systems (New York, London: Academic Press)
-
V. N. Sadovsky (1974), The foundations of general systems theory
(Moscow: Nauka)
-
N. Cutland (1980), Computability: An introduction to recursive
function theory (Cambridge, London, New York, New Rochelle,
Melbourne, Sydney: Cambridge Univ. Press)
-
C. Cooper (1994), "Complexity in C3I systems", Complexity
International, vol. 4;
online:
http://www.csu.edu.au/ci/vol1/Clive.Cooper/paper.html
-
A. Lerner (1967), The principles of cybernetics (Moscow: Nauka)
-
I. Prigogine (1980), From being to becoming: time and complexity
in the physical sciences (San Francisco: W.H.Freeman)
-
L. von Bertalanffy (1962), "General systems theory —
A critical review", General Systems, vol. VII,
pp.1–20
-
R. Goldblatt (1979), Topoi. The categorial analysis of logic
(Amsterdam, New York, Oxford: North-Holland)
-
L. Zadeh (1973), The concept of a linguistic variable and its
application to approximate reasoning (New York: Elsevier)
-
A. Kaufmann (1977), Introduction a la théorie des sous-ensembles
flous (Paris, New York, Barcelone, Milan: Masson)
-
H. M. Hubey (1996), "Special classes of fuzzy truth valuations
and probability theory";
online:
http://www.csam.montclair.edu/~hubey/papers.html
-
N. Wiener (1961), Cybernetics or Control and communication in
the animal and the machine (New York, London: MIT Press, Wiley)
-
M. D. Mesarovic and Y. Takahara (1975), General systems theory:
mathematical foundations (New York, San Francisco, London: Academic Press)
-
P. B. Ivanov (1996), "Computability in developing systems"
-
M.Mesarovic (1968), "General systems theory and its mathematical
foundations" IEEE Transactions on Systems Science and
Cybernetics, vol. SSC-4
-
H. M. Hubey (1996), "Intelligence, regression, multiplicativity,
path integrals, and stochastic models of scaling and evolution";
online:
http://www.csam.montclair.edu/~hubey/papers.html
|