Economy and Gravitation

by P. Ivanov
May 1999

Most people treat economy as a "social" science, in contrast to "natural" sciences dealing with much more certain and better tractable objects that do not need human intervention to be what they are. Though modern economy extensively employs mathematics, sometimes to the degree of an utter incomprehensibility, this usage rarely goes beyond the level of empirical regularity, predominantly limited to statistical analysis and stochastic simulation, as the fundamental economic forces still escape clear comprehension. The nature of economy is as obscure today as it was two hundred years ago. Just look at the row of Nobel Prize winners: their theories are nothing but political speculation upon an arbitrary qualitative dependence, at best supported by some empirical evidence, but never a consistent dynamic principle. Those theories that study the origin and general principles of economic relations do not provide any practical procedures to determine the quantities of interest, nothing to say of relating them to the traditional monetary evaluation. The same is true about their great predecessors, like Adam Smith or Karl Marx. For instance, Karl Marx' theory of value as a measure of the objectively necessary labor time is fine in qualitative analysis, but there is no way to numerically express that objective necessity. Though such a technique might eventually be suggested, currently, we have nothing to count but our hopes.

Physicists are especially proud of their exceptional role in the scientific study of nature, and they look at all those quasi-rigorous humanities with an undisguised contempt. Of course, a true scientist will never care for the opinions of the outsiders; any science must follow its own ways. Still, just for curiosity, one could wonder if some aspects of economy were resembling physical systems in their inner dynamics rather than in a merely metaphorical sense. When it comes to comparison, the first impulse is to turn to such branches of physics as thermodynamics, or quantum theory, as their statistical apparatus resembles the traditional economic numerology. However, the whole construction of modern physics is built upon the classical Newtonian mechanics, and trying to assimilate higher stories without recourse to the basics will hardly ever result in anything but superficial metaphor. That is why the best way to establish a solid link between economy and physics is to suggest a purely mechanical analogy.

But all we have in classical mechanics is material bodies (masses) moving in a Euclidean space under the action of some forces. That is, in economy, we need to find something like physical space, an analog of a moving mass, and a source of economic forces. Of course, this would require a thorough reinterpretation of the physical notions, adjusting them to the realities of the new domain.

At first sight, the mission seems utterly impossible. Economy is not physics; indeed, in some respects, it is very much different. All economic quantities we know are measurable in money and hence are essentially of the same kind: there are no capitals that could not be merged. All distinctions we make are like different mappings of the same continuum, and there is no perceptible need in more dimensions. That is, any physical quantities (both geometry and masses) must be constructed on the same monetary basis. Nothing to say about the definition of an economic force.

Well, if there are no direct analogs, we'll have to seek for nontrivial solutions. Economic space and time may well be unrelated to physical space-time, save by a formal resemblance. Thus, such apparently different phenomena as a pendulum, an electric current and the motion of a planet are described by the same idea of harmonic oscillation, with the same mathematical background. That is, to start with, we might take some fundamental physical law and reinterpret in in economic terms; this would give us a general background to guess for the details.

A convenient choice would contain all the principal mechanical quantities: distances, masses, forces. The famous law of universal gravitational attraction is the first and obvious candidate. Some economists may recall from school physics that any two material bodies attract each other with the force

,

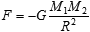where M₁ and M₂ are the masses of the bodies, R is the distance between them, and G is a fundamental constant. The minus sign means that the force is directed from one body to another so that in would tend diminish the distance between them. Sir Isaac Newton has endowed the humanity with this great formula, and its importance in our culture cannot be overestimated, since we owe to it a major part of our today's prosperity. Your reading these lines would be impossible without the astronomical discoveries and outer space technologies entirely based on the universal law of gravity.

Though we do not yet know any economic analogs of the physical quantities involved, after a little consideration, I could suggest a rather blunt solution, formulating the law of economic gravity as

,

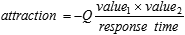or, in the symbolic notation,

,

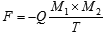where M (hinting to money) stands for some measure of exchange value (that is, I prefer to operate within the overall framework of Marxist economic theory), while the attraction force is denoted exactly like in physics, as we do not yet have a similar quantity in economy. The response time is an estimate of the time necessary to complete the assimilation of the invested funds; basically, one could think about it as return of investment.

To use the attraction law, we picture the whole economy as a number of possible economic positions that can be occupied by some economic agents (or businesses), and each agent is characterized by its economic value M. The agents may change their economic positions, and their economic value may, in principle, change as well. However, in a stationary economy (an economic system), the sum of all economic values is preserved despite the possible inner redistributions.

The qualitative acceptability of the suggested formula is rather obvious, and even trivial. Money makes money; and one capital tends to pool with another to do business right. The bigger is the capital, the more it attracts smaller investors; however, just like in physics interacting bodies act upon each other with the same force, the both interacting market values enter the attraction law in a symmetric manner, which is related to the formal equity of all the investors, regardless of the share. Of course, the core capital is much more economically influential compared to the army of petty contributors; similarly, we usually say that the Earth is orbiting the Sun, though, in fact, the both are rotating around the common center of mass.

Making fast money is normally more attractive than long-term investments; that is why the attraction force is proportional to the inverse of the response time. In the ideal case, when an investment brings an immediate profit, economic attraction becomes formally infinite. In reality, of course, there are no instant dividends, and no infinite attraction.

The usage of the first power of the capital rotation time in the denominator of the economic attraction law instead of its square (compare with the squared distance in the physical prototype) needs explanation. Though there is no obvious analog of a spatial point in economy, a certain feeling of distance between different businesses is commonly perceptible. One could associate this distance with the response time needed for a momentary investment in one business to influence the economic value of another. This results in a picture of the propagation of financial fluctuations, a kind of natural redistribution of any deviations from a stationary state. Similar processes can be readily found in physics as well, and they are basically described as diffusion, with many stochastic displacements (due to local interactions, collisions) resulting in a larger-scale drift from the original point. Thus, a drop of paint is gradually spreading in a pool of clear water; the aroma of a rose reaches our nose due to the same mechanism (in the absence of the wind). Market exchange could also be considered as a kind of diffusion, as it makes value travel from the original source due to multiple (almost chaotic) acts of trade. This is how financial fluctuations normally dissipate.

However, we know from physics that, in all kinds of diffusion, the average distance from the source is proportional to the square root of time elapsed. In other words, the square of distance is proportional to time. This justifies our choice for the form of economic attraction law. Alternatively, this can be considered as the definition of economic distance quite similar to physical space:

.

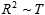Indeed, consider value propagation from business 1 to business 2, and them from business 2 to business 3. The total propagation time will obviously be the sum of individual times:

.

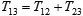But, in the terms of economic distance, we obtain

,

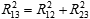which is exactly the usual Pythagoras' law for the addition of independent displacements in a Euclidean space. Geometrical orthogonality is, therefore, an expression of economic incompatibility, the necessity of sequential ordering and impossibility of parallel development. This gives clues to constructing economic frames of reference, the formal spaces to represent the available economic positions. We need to break the whole of the economic process into logically separate stages, thus representing it as a sequence of reproduction steps; these stages will determine the spatial dimensions of the economic model.

For instance, a common production cycle consists of three basic phases:

1. first, one needs to supply all the necessary items to start with (like raw materials, equipment, workforce etc.); this will certainly require some effort, which (in Marxist economy) is measured by some objective consumption time related to the price;

2. then the process of production must complete in the due time, to bring some trade value (measured by the values consumed plus the added value related to the objectively needed production time);

3. finally, we need to deliver the goods to the clients and receive their payment, to enable the next cycle of production; this is usually done through various market mechanisms.

Of course, in this idealized picture, the individual stages are only separable in respect to a single instance of production. In real life, we know, there are numerous economic schemes to reduce the effective times and thus increase the turnover. However, the common principle of most such schemes is to arrange for a parallel development of many elementary production acts, and one could consider them as the next level of hierarchy, merging the standard sequential operations in a statistical ensemble that can manifest a kind of collective effects. As the experience of physics indicates, such complex systems can often be described properly aggregating many elementary interactions, so that the behavior of the whole would follow from the properties of its virtual components. Similarly, our simple "mechanical" production scheme could serve as a basis for more realistic models in economy.

This sequencing determines a 3-dimensional space, so that any economic agent is characterized by three numbers (spatial coordinates) and the squared total distance between any two agents equals the sum of squared distances along the individual axes. As known from school mathematics, any sequence of three numbers determines a vector, characterized by both its length (the total distance) and direction. We can choose any agent for the reference point and construct a reference frame (a coordinate system) evaluating the distances of all the other agents to the chosen one. That is, the position of any agent in this space will be indicated by the vector pointing to that position from the origin. Obviously, any other choice is as admissible, so that there are many economically equivalent coordinate systems, shifted relative to each other in any direction by a constant distance. In some cases, an economic system would be better described by a different set of independent parameters (a different sequence of three stages); this corresponds to the rotation of the coordinate system.

Note that such a spatial placement does not concern the nature of the economic agents, and their coordinates do not tell anything about the character of their business. Such details are to be considered separately, using an appropriate economic model; a mechanical picture needs only coordinates and masses of the moving bodies, and it does not matter whether a mass of 1 pound is a bar of gold or a package of rice. This approach is well justified by the traditional economy considering the worthiness of an article as irrelevant to its exchange value, so that any capital could be expressed in the same monetary units.

The above 3D picture of production may be simplified in some practical cases. Thus, if we do not need to care for supply in the conditions of enough stock or stable delivery, we can omit the consumption stage, effectively reducing the problem to two spatial dimensions. Similarly, for highly demanded products, the delivery phase is no longer important, and we get a simple one-dimensional model tractable with some standard mathematics. In this manner, many economic processes are reducible to simple oscillations, provided we know the nature of the acting force. However, the law of economic gravity is not of much use in a one-dimensional case, since all we can get in such a model is merging the individual capitals together, sooner or later. Though considering such a collapsing economy may be of some practical importance, a more dynamic picture needs at least two dimensions, to allow for complicated orbits and all kinds of stationary solutions. Since the attraction law takes exactly the same form as in physics, we expect to find some economic analogs of the well-known astronomic phenomena.

Just for illustration, consider the case of simple reproduction within a limited economic domain. As the added value can be neglected, the production stage averages out, and we get a two-dimensional system with one dimension (let us denote it as x) corresponding to economic consumption (the demand dimension) and the other (denoted as y) related to product distribution (the supply dimension). A stationary motion in such a system requires a dynamic balance of supply and demand, and the evolution of an individual business is represented by a trajectory in the configuration space. An elementary transaction (an analog of physical displacement) will change both the level of demand and the level of supply (which is quite natural, since something bought is, in the same time, something sold):

.

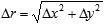A sequence of such transactions defines local economic time (denoted as t; note that it does not coincide with the physical time), and we can define the vector of economic velocity characterized both by the transaction rate (the "speed")

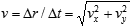
and the direction (related to the ratio Δx / Δy). If there were no economic forces, each economic agent would move straight in the same direction, gradually raising the turnover up to infinity (which is not too realistic, is it?). However, if there are two agents 1 and 2 with the respective economic values and the attraction force in action, the picture is quite different. Thus, if the capital 1 is much greater than capital 2, and the velocity of 2 in respect to 1 is not too high, we obtain a stationary motion of agent 2 along an ellipse around agent 1 placed in one the focus points. The attraction force, of course, is always directed towards the agent 1, but the speed of agent 2 and the direction of its velocity periodically changes within some reasonable limits:

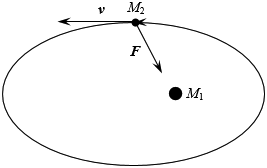
Thus two capitals form a compound system that can behave as a whole in respect to some other agent who cannot discern the details of the inner motion from far away. Obviously, a huge capital (a star) can attract numerous small companions, forming something like the solar system including the planets of all sizes as well as a lot of cosmic junk like asteroids, comets and clouds of dust. Just like in astronomy, two capitals of comparable sizes can form a double system rotating around a common center of mass, possibly with many smaller companions of a planetary scale. An important qualitative prediction of this models is that close triple unions must be much fewer in economy than double companionships, as such many-center systems are less stable. However, just like in the outer space, many distant (and weakly coupled by gravity) economic agents can form a kind of stellar associations that may either dissipate in space or evolve to some compact conglomerates.

Already in this limited model, the law of economic gravity can be used to explain many quasi-stationary effects in a stable economy. Combined with the dynamic laws related to other economic forces, this theory might become a powerful tool of economic research. Moreover, it is paradigmatically important, since it can serve as a starting point to develop complex conceptualizations better suited to describe the processes in real economy. One could already have noticed that the introduction of economic distances involved a reference to microeconomic processes quite similar to those described in terms of motion in thus obtained macroscopic kinematics. In particular, the growth of capital is related to the accumulation of the added value in extended reproduction. In a stable economy, masses of any agents may change, provided the total mass (the bulk of the public wealth) remains the same. A growing economy assumes both the increase of the capital (mass and energy production) and the broadening of its scope, the expansion of the economic space quite similar to the well-known cosmological expansion in physics. To properly describe this non-stationarity, one will need an analog of the relativistic theory of gravity, with matter producing space-time and space-time producing matter.