The Diagonal Fallacy

The formality of mathematical knowledge is both its principal advantage and the major source of conceptual problems. While a mathematician is engaged in studying a particular mathematical object, he may (like in any other science) never worry about the correctness of the typical operations. Still, any attempt to formally describe the very formalism, to scientifically study the method of science, is bound to fail from the very beginning. Such a formalization will necessarily be incomplete, since it pays attention to a specific aspect of the scientist's work, while abstracting from the numerous informal procedures, which only can render science meaningful.

The foundations of mathematics lie beyond mathematics, and no metatheories can help. This is just another level of reflection, which is entirely outside the scope of science as such. No doubt, every activity involves a number of formal components that could be squeezed into scientific standards, so that everybody could learn them. In a way, all science is a factory of technologies, typical schemes of activity that can be reproduced in very different situations, including the development of science. The scientific product is a kind of huge textbook, a cookbook containing millions of life hacks, to conveniently rule out most everyday problems. In this respect, mathematics is in no way different from chemistry, political economy, anatomy, choreography or rose planting.

The discrimination of a formal structure in a real activity assumes a certain level of abstraction dividing all the aspects of reality into those that are relevant and those that are not. Such levels are not arbitrary in the history of culture, though a general regularity does not remove variations of any kind (which, in their turn, form a hierarchy of formality or meaningfulness of their own). It is important that different levels exploit different formal features, and there is no final, frozen knowledge, since (at least) new representations of the same are always possible, and we need to adjust the well-established theories to unexpected practical needs.

Formal knowledge is only viable within a single level of hierarchy. When a mathematician tries to formally join several distinct levels, this comes up as a contradiction.

The famous Gödel theorems provide a popular example. They have been given a lot of formulations, sometimes very far from the original arithmetic approach. A common reader will find these theories too technical, as they are oversaturated by minute detail and highly suspicious artificial constructions ad hoc. This resembles too much the machinery of a circus magician designed to distract the attention of the public from the insides of the trick.

Still, the affair is quite transparent. Any formal system can be represented with a number of statements somehow assigned with the logical value "true" or "false". If some statement happens to receive the both marks, the formal system is called contradictory. But this only refers to the structural level. To make a system, we need to specify its input and output, as well as the method of obtaining the result from initial data according to a number of rules that constitute the inner structure of the system. The structure of a formal system is determined by the derivation rules to obtain a true statement from a number of other true statements. Of course, one can apply the same rules to false statements, but this will tell nothing about the truth of the result. In this way, any formal system is enhanced with the notion of deducibility, and we have to investigate its relation to truth valuation. In particular, a formal system is called complete, when every true statement is deductible.

Obviously, deducibility is like higher-level truth, the next level of hierarchy, known in dialectical logic as the negation of negation. Unlike the immediately true statements, deductible statements are not only true by themselves, but primarily, true by derivation. In practice, it is always possible to either make a particular statement an axiom or derive it from other axioms; these are the different ways to unfold the same formal system, thus producing its hierarchical positions. In any case, truth and deducibility belong to different levels, and their mixture within the same context would be an instance of inconsistency, a fallacy. Now, this is just what all the forms of the Gödel theorem attempt to do!

In the core of the trick, we find the so-called diagonal principle: a statement gets separated from its content, from the object area, and is declared to apply to anything at all, including itself. For a few millennia, logicians reproduce the same old liar paradox, adding ever more interpretations in the popular literature.

The proof of the Gödel theorem (in any formulation) involves artificially constructing a reflexive statement meaning: "every deductible statement is false". If this statement is deductible, then it is both true and false, and the formal systems is contradictory. But, if it is true, it is not deductible and the formal system is incomplete.

That does it. All one is to clarify is how the conjurers fool the happy public.

For this purpose, mathematics (following the lines of philosophical positivism) employs a standard trick: the content of a statement is identified with the form of its expression. A sane person will hardly ever mean it. When we say, "the egg was boiled during three minutes", we mean that very egg, and the boiling water, where it spent three minutes according to the kitchen timer. But never the sequence of words used to tell that.

A mathematician acts in the contrary manner: he declares that any formal statement exists insofar as it can be expressed by means of some formal language, and all the statements can be enumerated as soon as we have fixed the alphabet. The possible translation from one language into another is then reduced to mere substitution of the original characters for new ones according to a definite rule, which does not deny the very possibility of enumeration.

Sounds convincing. The public is enchanted with the artful movements of the magician explicitly constructing the language and formulating the theory, which is to eventually bring in the desired diagonal formula. Apparently, the Gödel theorem is an elegant mathematical result, a revelation of supreme science.

With all that, it is exactly science that it lacks. Science is always object bound, it studies something real and never asserts anything in general, but solely within its application area. If we start paying attention to the mode of producing and presenting scientific facts, we immediately switch to a different object area, that is, from one special science to another. We have no right to confuse the notions of different sciences, however similar their statements may sound; such a confusion would mean a banal logical fallacy called term substitution: the same word (symbol) refers to different notions within the same discourse.

In fact, this is the essence of the genial Gödel's idea, to encode all the statements (identified with their formulations) with integer numbers, along with the rules of derivation, so that any statement at all gets reduced to a statement about numbers. But numbers are always numbers, even in Africa; we can compare them in any way, including the diagonal technique. The nature of this logic could be illustrated by an example: let all the even numbers refer to the statements of edible things, and all odd numbers refer to something non-edible; then we can shop for two non-edible things and have a good breakfast just putting them together...

The fraud is even more evident in the following formulation: since all the words are composed of the same characters, they all mean the same.

While mathematics keeps with science, that won't pose any problem. Every schoolchild knows: each function has a particular domain. For an inadvertent deviation from the appropriate domain, one gets a bad mark at exam. Still, as soon as a mathematician graduates from the high school and proceeds with a career of their own, one can forget about such minor nuisances. Thus, in category theory, many theorems can be boldly proven in the assumption that all the arrows are properly defined in some sense. In the end, we get a result serving to explicitly specify the properties of the arrows presumed from the very beginning. Here is yet another popular fallacy, logical circularity, the other side of the diagonal principle.

A scientific theory is to construct meaningful statements about some application area and establish their adequacy within that very area, that is, their truth. One could formally picture it as a truth function defined on the universe of all the acceptable statements X:

,

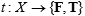where F and T are the available truth values (in some cases we need more choices). In real life, this representation is not always valid; but let us accept it for a while. Under the same conditions, deducibility formally defines yet another function:

,

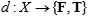admitting that

.

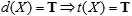Omitting the detailed specifications, the fundamental Gödelian statement can be expressed as

.

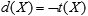But the last two functional formulas do not belong to the domain of the functions t and d; their domain is the space of all functions over the universe X, which needs an entirely different science... And possibly, it is no science at all, if we fail to indicate the object area it pretends to describe.

The mathematical trick of the Gödel theorem, the amalgamation of incompatible statements within the same theory, is widely used in other mathematical sciences. It is enough to recall the great theorem about the stationary point considering the mappings of an n-dimensional ball onto itself

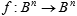
and stating that one can always find a point x, for which f(x) = x. The trick is to blend the domain and the range of a function, though, to remain within science, they can hardly ever coincide, since (using the physical terminology) they are measured in different units: [x] ≠ [f]. Roughly speaking, they stand on the opposite ends of an arrow, and this positional difference makes them qualitatively different. The very admission of some portion of space transformed into itself is already a petty cheat, since two different aspects (or applications) of the same are thus identified. In any case, such a reduction of the range of a function to its domain is, in general, a nontrivial operation operation never imaginable inside mathematics; science borrows such acts from praxis. If, in everyday life, we can convert the products of our activity into the raw material for the same activity, you may justifiably use your formalism. If such a reproduction is limited, just be careful with your conclusions. That is why we always need to experimentally test our theoretical predictions which remain mere hypotheses (however necessarily implied by everything we already know) until they are practically proven.

The identification of the range of a function with its domain is akin to the already mentioned fallacy of term confusion. Indeed, even if it is possible to represent the values of a function with the same entities as its arguments, this apparently identical notation refers to different things. You may wish to mark your fingers with the decimal digits 0 to 9, and do the same for your toes; still, your fingers won't become toes, or the other way round. It is not an easy deal, to make fingers and toes really interchangeable (though, in some particular cases, one can achieve that).

Mathematicians use the word "isomorphism" to justify the tricks like that. It is enough to pronounce the magic incantation that the range of the function coincides with its domain "up to an isomorphism", to drop any further concerns. But, in the real world, to use the output of a system as its input, you need a quite material feedback circuitry; without this practical feedback, reflexive mathematics is of no use. Luckily, the development of mathematics never follows the whimsies of its grands, better listening to the public needs and practical feasibility. Indeed, any time something enters the head of a mathematician, it certainly does not emerge from nothing, and there is a cultural reality that has induced it. However, this reality may be of a peculiar kind, not necessarily in a positive sense. Thus, a mathematical idea may be an expression of a common (methodo)logical fallacy.

For yet another illustration, let's recall computers. Many programming languages distinguish values from their types. For instance, the number 1 in integer arithmetic is not exactly the same as real or complex number 1; they may be denoted by the same character in the language (using the dynamic typing mechanism), but their inner representation will be different and have nothing to do with the corresponding ASCII code, or the string "1". In object-oriented programming, types are represented with classes, while values refer to the instances of the class. A class may have any number of instances, which remain separate objects independent of each other. Still, all such objects are "isomorphic" to each other since their inner structures (fields and properties) coincide, and they allow the same operations (methods of the class). Just try to confuse two objects of the same type in a computer program! You are sure to have a heavy debugging session, and any possible headache. Mathematical bugs are more difficult to trace, though they are basically of the same origin. There is also a psychological effect: the wide public tends to yield to the demonstrations of mathematical "rigor", up to the utter incapability of doubt in the face of some perfect "proofs". This is especially so considering the fact that few people are educated enough to understand mathematical discourse, which is packed up with the references to somebody else's results, to be accepted as a matter of belief.

Well, let us get back to science. I stress once again that any science is to produce statements about some application area, meaning that such statements could be further examined to establish their validity or truth (which is not the same). Traditional mathematics would arrogantly declare all such statements as firmly established, once and forever. That is, any science is only meant to "discover" all kinds of truths. Real life is a little bit different. The development of a science is a complex and dramatic process; there are different directions of research, and one can never predict the outcome of a particular choice. The application area of a science does not exist on itself, like Plato's ideas; it grows along with the growth of the science. To illustrate it with something simple enough, just within the grasp of a mathematician, consider that the statements of a theory are yet to be built out of its elementary notions. These notions may be either adequate or not so perfect. Similarly, one can construct statements of notions in an either correct or incorrect manner; that is, there are things that can and that cannot be asserted in this particular science. One does not need a microscope to observe that this is yet another instance of the same Gödelian scheme: some meaningful statements are bound to be inexpressible in the terms of the theory, or contradictory. To raise an incomplete and contradictory logic upon such an incomplete and contradictory basis, isn't it just a little bit strange?

In this context, the "linguistic" trick is no longer entirely convincing. Why do they think that the alphabet is fixed for all times? Things like that rarely happen in real life, where we need to invent more and more signs for anything that just did not exist before. In particular, such sign creation can merely reinterpret the already existing signs, using different interpretations in different contexts. The effective number of characters will thus grow to infinity, while we are still capable of encoding these characters with a finite alphabet. A finite code can refer to (or represent) something infinite, depending on the context, while the number of contexts is in no way limited. With all that, Gödel's arithmetization of logic becomes utterly unfeasible. So, one has to honestly admit that mathematics is a science like any other, with mathematical theories valid only within the area of their applicability, limited to the objects of a certain kind. No more royal pretense; like physics can hardly pretend to be the theory of everything.

Right there, in a truly scientific research, the diagonal principle happens to be quite useful, provided we do no exaggerate the generality of our conclusions. And we can, in certain practical cases, identify isomorphic spaces. Or build, within a limited range, recursive theories and programs. However, if the ends do not meet, and the result seems to be far from the common views, one should not just take the posture of a prophet and blame the dullness of the folks; maybe it is something in the mathematical reign that went wrong. In the latter case, we'll need to drop out some apparently evident identifications and carefully place mathematical constructs in the appropriate levels of hierarchy. Just to introduce some space for mathematics to expand.

Aug 2009