Fuzzy Sets and Relativistic Velocity Addition

The axiomatic skeleton for fuzzy set intersections i(a, b) and unions u(a, b) is given by:

1. boundary conditions:

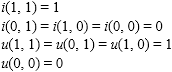
2. commutativity:

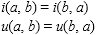
3. monotonicity:

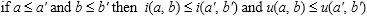
4. associativity:

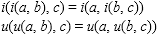
In general, fuzzy set unions and intersections are not idempotent. Every possible choice of the form of fuzzy union, intersection and complement would violate at least some properties of the Boolean lattice. In particular, the law of excluded middle and the law of contradiction may not hold.

As it is well known, the conditions 1–4 lead to inequalities

,

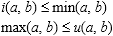so that i(a, b) < u(a, b) for a ≠ b. The most common form of fuzzy set complement is c(a) = 1–a.

One could easily construct an example illustrating that the axioms 1–4 may be incompatible with DeMorgan’s laws:

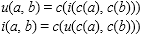
Indeed, let us assign to every element x_i of a fuzzy set 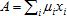a number 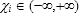such that

.

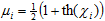With χ varying from –∞ to +∞, μ monotonically increases from 0 to 1. Let the complement of A be constructed according to the usual rule:

.

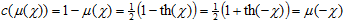Finally, let us define the intersection of two fuzzy sets as

.

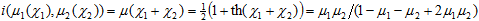This expression satisfies the boundary conditions for fuzzy set intersection; it is evidently commutative and monotonic. Direct computation shows that it is also associative:

.

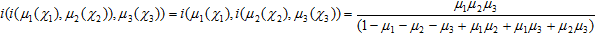Thus defined i(μ₁, μ₂) is however not idempotent, though it is asymptotically idempotent at χ → ±∞, which ensures a correct transition to ordinary (crisp) sets.

Now, let us use DeMorgan’s law to introduce set union through intersection and the complement:

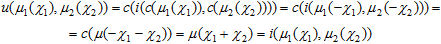
Since thus defined union and intersection coincide, set union will not satisfy the axiomatic skeleton, violating the boundary conditions at  μ₁ = 0  and  μ₂ = 1 . And, of course, the value of  i(μ₁, μ₂)  can never be less than u(μ₁, μ₂) as it should be from the skeleton axioms. It should be noted, that the law of excluded middle and the law of contradiction are not satisfied for this choice of intersection/union:

The physical sense of the above definitions is relativistic addition of velocities. The particles moving forward with the speed of light are associated with μ = 1, while those moving with the speed of light in the opposite direction are associated with μ = 0. Note that the definition of union based on the addition of only positive velocities

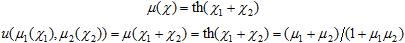
is known as a function of the Hamacher class with γ = 2, and, together with the standard complement, it produces the intersection

,

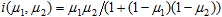so that both the axiomatic skeleton and DeMorgan’s laws are satisfied. However, in this case, the definition of the complement is “physically incompatible” with the definition of the union, since Galilean velocity addition principle is mixed with the relativistic rule.

14 May 1997