Negative Sets
All fundamental mathematical objects are nothing but an abstract expression of the typical modes of activity. Thus, integer number originated from the procedure of counting and recounting, with the result that happened to never depend on the enumeration order. On the contrary, negative numbers express the idea of the impossibility of counting, of lack, or debt (so that the usual sign multiplication rule becomes related to the custom of debt compensation or paying off). Later on, when the overall idea is clear enough, one can get engaged in constructing formal models; thus number theory come to light, with its peculiar theorems.
The idea of a set is an abstraction of inclusion, of the possible involvement of an object in some human activity. When we set about doing something, we first look at what could be useful for that, and what would impede it. All we see gets evaluated from this viewpoint. This is an entirely qualitative assessment: if it does for our purpose, we’ll keep it in the mind; if it won’t do, just drop it and don’t care any longer. Formally, we speak about an element belonging to a set, meaning our ability of constructive check. A set is exactly the entirety of what in contains, and it has nothing to do with the rest. In other words, it is only the property of belonging that is properly defined, while not belonging is something most uncertain (just because we cannot know everything in the world, including what is yet to come). However, when our activity is a part (a stage) of another activity assuming a wider range of objects to involve, the property of not belonging can be taken in a narrow sense, as belonging to a complement. This is a quite testable hypothesis.
In general, rather complex hierarchical structures can emerge in this way; this reflects the diversity of human activity. Non-belonging is differently defined in different contexts. Still, in any case it refers to belonging to something else. Mathematicians prefer to deal with a constructively defined "universe" and never touch whatever lies beyond. This perfectly matches the natural circumstance that we always work with what we have, which is here at hand and is (at least in principle) available.
However, in real life, besides the things that are fit for the current activity we often encounter things that are incompatible with it, or practically inaccessible. With that which is somehow present but cannot be used (is "forbidden"). Such objects are essentially related to the activity, they belong to it as well, but in a "negative" manner. These are not elements, but rather holes, the indicators of the necessity to exclude some things from consideration.
The term has been borrowed from physics, where electrons and holes productively co-exist in atomic models, in semiconductors, and in many other practically important areas of research. In a way, a positron is nothing but a hole in the vacuum produced by the ejection of an electron; that is why electrons and positrons are always born in pairs. We find that the idea of a hole leads to a practically attractive mathematics in set theory.
As we already know that the complement may play the role of subtraction for sets, we can formally define a negative set as the complement of a regular set to the empty set, as its subtraction from "zero". The existence of such a complement can be simply postulated. We express it as 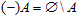 . The minus sign has been put in parentheses to stress its operator nature. By definition, every element of the negative set is a hole in the position of a presumable element of the original set. Obviously, . The minus sign has been put in parentheses to stress its operator nature. By definition, every element of the negative set is a hole in the position of a presumable element of the original set. Obviously, 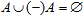 . That is, considered together in the same activity, the element and the hole will "annihilate" each other, so that we have neither inclusion, nor exclusion. Symmetrically, . That is, considered together in the same activity, the element and the hole will "annihilate" each other, so that we have neither inclusion, nor exclusion. Symmetrically, 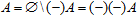 . In this way, we fix the logic of the theory; in some activities, this condition may not necessarily hold. . In this way, we fix the logic of the theory; in some activities, this condition may not necessarily hold.
Observing that sets are not linearly ordered like numbers, we can extend the study of regular and negative sets to the general case of arbitrary collections of elements and holes; for simplicity, we keep calling them sets (or classes, if you wish). Clearly, a general set can be decomposed into the "positive" and "negative" parts:
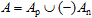 , ,
where Ap and An are regular sets (just elements, without holes). In particular, they may be empty. In a union of two sets, the corresponding elements and holes annihilate:
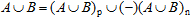 , ,
with
 , ,
A less trivial mathematics comes in as we pass from addition to multiplication, from the union to the intersection of sets. Here, formal evaluation requires the introduction of the common sign multiplication law: 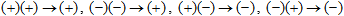 . The double negation has already been mentioned; basically, it can be translated as "the absence of absence is presence". In the same manner, we understand both the presence of absence and the absence of presence as absence. Once again, this is not always so in real life, but it will do in many importance cases. Then, obviously, . The double negation has already been mentioned; basically, it can be translated as "the absence of absence is presence". In the same manner, we understand both the presence of absence and the absence of presence as absence. Once again, this is not always so in real life, but it will do in many importance cases. Then, obviously,
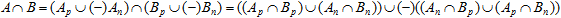
Thus, one could construct a special case of an "antiset" of an arbitrary set:
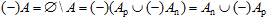
From the quantitative viewpoint, regular sets are characterized by the number of elements, assuming that each element contributes +1 to the total. Negative sets obviously imply the number of holes, each contributing –1 to the number of elements, so that the potency of a negative set is negative. For a general set, one needs to sum the positive and negative contributions, and any combination is possible.
In applications, holes may become a promising formalization of the notion of need, which is practically important in sciences like psychology or economy. On the other hand, noting that particle annihilation in physics leads to the production of new particles, some quite nontrivial theories of activity could be developed. By the way, the notion of element is one of the most elusive in the present set theories; one can hardly tell it from a set. Traditionally, mathematicians tend to identify elements with sets thus limiting themselves to narrow range of the possible theories. One could observe that any object as an element is nothing but the class of all the sets containing it; conversely, as a hole, any object is associated with a class of sets it does not belong to.
Any mathematician will readily indicate the algebraic structures covering the above, and proceed to the far-fetched conclusions. Here, we are not interested in the formal details; we rather seek for an intuitively pleasing notion of qualitatively distinct mathematical object. Such fundamental objects cannot be reduced to each other, even resembling each other so much. Thus, one could derive mathematical logic from set theory, or vice versa; the both will keep their special ways. Real numbers modelled with convergent sequences of rational numbers will remain real; even if we identify them as the elements of a field, this will result in yet another (general algebraic) model, abstracted from any other (possibly as important) aspects. Real numbers do not come from math; they come from praxis. Just like integers, or complex numbers, or geometric shapes, or sets.
Now, we get negative sets. Proceeding in this direction, one can construct complex sets, or spaces of an arbitrary dimension... Let it be postponed to a better time.
Dec 1984
|