Quantum Set Theory

The fundamental notions of the classical set theory are never formal: a set, an element, membership and absence, equality and difference... Depending on the conventional usage rules, different classical theories may emerge; in any case, the formal axiomatic carcass cannot be treated as a definition, but rather should be taken for a "constraint" (in the sense of theoretical physics) narrowing the range of the relevant constructs, while never eliminating terminological ambiguity. When it comes to drawing analogies from physics, we have to operate within a specific interpretation; this is a regular situation in any science and it does not pose any serious problems as long as no abstraction is deemed to be absolutely preferable and the natural scope of a particular science is always kept in the mind and respected. On the other hand, all the possible models are equally admissible, and one is free to expand whatever, however exotic, in the hope that the experience might come handy on an occasion.

Traditional mathematical objects are essentially static: they are just somehow given, and a mathematician is only to study the already available features. Well, this is exactly like we used to look at the world before the XX century, under the reign of classical physics. A set thus understood is an outer thing on itself insensitive to all kinds of manipulation. Somebody we don't know has made it for us that way, and we can count on that it won't change or disappear while we are still working on it. Accordingly, given several sets, we can cook them all at once and the result will be as eatable for anybody else.

For every set, the presence of elements is the principle #1. We do not mean that some other entities cannot have elements, they too; still, an entity without elements can be anything but definitely not a set. In particular, the phrase "empty set" is nothing but an abbreviated form of a statement like "there is no set such that..." In an appropriate context, this negative existence may acquire certain trait of an object (with a variety of equally admissible paradigms), but that won't in the least make it a set.

One set is not like another. When it is small, we can enumerate its elements one by one or grasp them all at a glance; in the worst, we can suggest an effective procedure for sorting them out in a final (within a current activity) time. For very big sets, this is no longer an option; the maximum we can hope for is to find an illustrative analogy: it is like a segment of a curve, a collection of functions etc. For some sets, we cannot afford even that; there is an opinion that such huge conglomerations should not be called sets proper. All right, let's pretend to have got such a monster, one way or another. Now, there are two problems: first, anything relatively well-formed we encounter in our life may be or not be an element of a given set; that is, there must be an effective procedure to determine the membership of anything at all to our (however large) set. Second, declaring it to be a set, we must be able to support our words explicitly presenting at least one of its elements to the public; in other words, we need a practical ability of plunging the hand into the set and getting out ("selecting") something that would undoubtedly be recognized as belonging to it (moreover, specifically as an element, not just a subset). The both procedures may come highly nontrivial; indeed, it is the technologies of the kind that any branch of classical physics is to eventually develop: every science is to historically grow to a clear recognition of its object area.

Any idea of membership in the classical set theory comes from explicit set construction, that is, given a well-defined object we only restrict (directly or through imposed constraints) the right of different object to belong to a given set. No comprehensive universe can ever be defined within set theory; any known attempts have always lead to a logical circularity, the premises exploiting the features of what is to be eventually obtained.

With sampling, things are no lighter. Admitting that we can be satisfied with a conventional technology, there is still a possibility of sets differently reacting to what we do: no arbitrariness, no mathematician's caprice, but rather the demand of the object area we mean when using that very kind of mathematics. The traditional set theory deals with collections that cannot contain an object of a given type more than once. When we draw out an element in the course of sampling, we obtain a different set that does no contain that very element. In other words, a set as an integral whole splits (decays) into two parts: an element and the residual set (absent in certain cases). We are well acquainted with such transformations in physics and chemistry. Of course, in that picture, human intervention in a mere locution, and we can as well consider interacting sets interchanging elements due to some objective happenings, in an entirely automated manner.

The complementary approach is to allow several elements of the same kind within a single aggregate, which should not probably be called a set, but rather a "bag". Provided there is an effective procedure for determining the number of identical elements, the bag will virtually be a set; in general, this is not the case. For set-based bag, one still has opposite choices. For instance, take a two-level structure, with the elements well-distinguishable on the lower level, but merged in equivalence classes on the upper level. On the contrary, in a statistical representation, we speak about the probability of an element's membership in a set: the number of identical elements is effectively divided by the total number of elements. For very large sets, the statistical approach may be preferable (and even the only possible). Any intermediate structuring would involve some generalized statistical weights and the corresponding statistical sums; practical considerations stand behind a particular choice.

With all the diversity of paradigms, classical set theory refers to some "accomplished" sets that can be studied at any convenient pace. For a classical observer, any structural change will look like a "singularity", "catastrophe", or "phase transition": the end of a world, and the beginning of another. Here, we are interested in the smooth evolution within the zones of continuity; in their meeting points, any stable structures are assumed to completely form during the time (or instant) between the two consecutive acts of "measurement".

A quantum experiment is primarily different from a classical setup by the observer's intervention in the motion of the system to be observed: first, we prepare something observable, and then try to figure out what we have really prepared. Classical experimenting is following that scheme too, but the classical act of creation is in no way related to the process of observation: the two activities are well-separated in space, time, or however else; roughly, an already prepared system lives long enough to forget about those who gave birth to it well before somebody else would wish to study. A quantum system is consumed immediately, in the very time of its arrangement. Similarly, a movie differs from a stage show, correspondence from live talk. As usual, there are minute gradations, and the distinction of quantum and classical sets can only exist on a specific level of hierarchy unfolded in one of the possible directions.

Quantum dynamics proceeds entirely inside a classical singularity point; for a quantum description, the whole classical motion before and after restructuration will serve as the initial and final state, the asymptotic conditions. The matter of the fact is in there, but we cannot directly observe it (without breaking a quantum system into classical parts) and hence must guess by the side effects, comparing the incoming and outgoing structures.

A quantum set (or, generally speaking, a bag) is a formally prepared system in one of the possible states; this can be conventionally represented by the abstraction of a "state vector" |A⟩. All sets that can be produced using the same preparation technique constitute a kind of universe: metaphorically, we call it a "configuration space". To determine whether an element a belongs to a set A, we compute the number (an "amplitude") ⟨a|A⟩, with the square of its modulus taken for the degree of the element's membership in the set (statistical weight). Using the same vector metaphor, one could consider an element as a "functional" over the configuration space of a specific level. The ensemble of such functionals will determine the object area of the theory. In other words, this is what we want to eventually get in the course of activity, its practical outcome, a product.

A one-element set containing a single element a could be denoted as |a⟩, with ⟨a|a⟩ = 1 (in general, the character "1" may stand here for something far from being a number; for instance, a kind of δ-function, that is, yet another functional). For all the other members b of the object area, ⟨b|a⟩ = 0.

So far, no significant difference from a classical set/bag theory have been introduced. The transition from probabilities to amplitudes does not change anything on itself; it is no more than a kind of substitution of variables, a change of viewpoint; with the classical weights of the elements as the only outcome, the benefits of the new formalism are rather obscure (if not doubtful). This will be so as long as we deal with the earlier prepared sets and do nothing except measuring the degrees of membership. Any kinematic picture is bound to expand on the level of macroscopic (classical) observer, since all we need from a science is a number of practical things ready to use in our everyday life. Essential differences can only be found on the level of dynamics: with classical sets, we combine the observables (statistical weights), while the interaction of quantum sets means combining amplitudes.

As we discuss mathematics, which is basically a science about abstract structures, dynamics cannot directly enter a mathematical theory and it must be represented by specific structures. Within the quantum paradigm, we associate any state change (motion in the configuration space) with "operators". Immediately, this concerns set transformations, that is, set operations defined on the current universe; however, any set comparison is also a kind of transformation, and hence various relations between sets must also be representable with operators, though possibly of a different kind.

In particular, the relation of an element's membership in a set requires reconsideration. The idea is blazingly simple: one cannot compare qualitatively different things (belonging to different levels of hierarchy). Elements are comparable with elements, sets with sets. To compare elements with sets, we need to somehow bring them to the same type. The traditional notation a ∈ A is a mere abbreviation for a sequence of nontrivial acts, each with their own conditions of feasibility. Most such assumptions never come to a clear wording: usually, a mathematician just believes that his abstract world is regular enough to justify any formal manipulations that lead to the desired result. Numerous logical strains drive some mathematicians to abandoning the very notion of an element, so that the whole theory is restricted to set comparison; this does not help much, just postponing the difficult questions that will come back elsewhere, in a new formulation.

In quantum set theory, sets are represented by "state vectors", while elements are represented by "functionals". The difference strikes the eye. Establishing any interrelations is quite an undertaking, with different technologies leading to very unalike theories. Still, in any case, we have two basic options: either elements are to be transforms to sets, or the other way round, sets to elements. The third way, bringing the opposites to a new synthetic entity, would virtually break the boundaries of set theory proper.

The former approach is possible using a special set operation, projection: its intuitive sense is to pick out a part of a set (or a subset, in the language of the traditional set theory). For a single element a, the corresponding projection operator is commonly written as |a⟩⟨a|, so that the projected set (the outcome of projection) would take be pictured as |a⟩⟨a|A⟩, which apparently puts each element (functional) in correspondence with an appropriate one-element set (vector). So, in a given object area, a set formally becomes a linear combination of one-element sets:

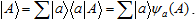
The same set can be considered in a different respect (in another object area), which would results in a new expansion of the same type:

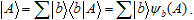
This "completeness condition" is often formally formulated as

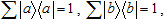
but we must keep in the mind that the configuration spaces for elements a and b need not coincide: in general, no transition from one "basis" to another is meant, as we can treat the same thing many alternative (or complementary) ways. For instance, a graph can be represented by a collection of nodes connected by arrows; but it can also be treated as a number of arrows connected by nodes. One can control a computer using a keyboard, in a command-line interface; but the same controls are often available in a graphical interface, with just a mouse click. In both cases the effect is the same, despite all apparent differences.

It should be noted that the dimensionality of a basis is not related to the size of the set. For example, in atomic physics, the same quantities can be evaluated by either an integral over the continuum states or a sum over a specially designed discrete basis. In logic, we use a two-element basis (just T and F) for a whole lot of the possible statements; their object content and practical meaning are irrelevant for logical valuation. Everybody knows, that the same problem can be solved using a standard but cumbrous approach, or in an unexpected and elegant manner.

Generally speaking, the product of an activity is different from its object (the raw materials and available technologies). Still, in certain situations, both the object and the product are considered in one of the possible aspect, so that the difference is effectively lifted. Thus, in market economy, both material and spiritual reproduction are regarded as the metamorphosis of exchange value; similarly, in the structure of a scientific theory, deduction moves from a number of truths to other truths.

In real life, an orthogonal basis is often more comfortable and illustrative; still, just like in classical theory, orthogonality is not indispensable: the presence of one element in a set may (to certain extent) mean the presence of another. In quantum theory, orthogonality means that every one-element set is a eigenstate of a specific operator.

The transition from one basis to another can be expressed as

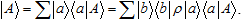
That is,

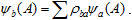
In the simplest case, when the basis spaces of a and b are defined in the same universe, the "density operator" ρ can become identity, and we speak about equivalent element representations of the set. In general, one still needs to bring one object area to another to ensure comparability; the way of such reduction depends on the intended applications.

Treating sets as collections of elements implies the ability of explicit construction. As in classical theory construction is well separated from observation, there is an illusion of the simultaneous presence of all the elements of the set: they all are in the view field, and no element can be preferred. Quantum set theory represents addition or removal of an element by the corresponding operators: the notation 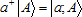means that, acting with the "creation operator" a⁺ onto the set A, we obtain a new set that is likely to (but, as indicated below, will not necessarily) contain the element a; we expect that . The inverse operation is to act with the "annihilation operator" a^– onto the set |a; A⟩, admittedly restoring the set A. Any finite extensions of a given set A can be constructed in this manner; here, the set A plays the role of "vacuum", a reference state for the rest of the theory. One might get tempted to take the empty set for the base and thus develop an "absolute" theory. However, the empty set is not really a set, and we should not treat it as a regular set, and, in particular, we cannot act on it with any operators defined for real sets. Similarly, in modern physics, vacuum is a sheer conventionality, a level of reference. Coming across a formula like a^–|0⟩ = 0, we must take it in the idiomatic sense, as an expression of the a variety of constraints imposed on the physical system; in many cases, annihilation operator for a particle a can be considered as creation operator for its antiparticle: 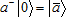, so that a system might admit states with both particles and antiparticles (like an electron-positron pair, or the coupled motion of the free electron and the ionic hole in atomic ionization). Nothing prevents us from considering 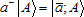as a set with a hole (an anti-element); the specific implementation of element addition or removal depends on the intended applications. For instance, adding an element to a set will not necessarily be a kind of creation: it may just increase the numbers of elements of the kind (like in the case of electron capture by an atom or an ion). In the same way, element annihilation may just diminish the "weight" of that element in a set, provided the element and the hole instantly annihilate leaving no trace of the event in the resulting set. In the simplest case, when the set is not allowed to contain more than one element of the same kind, creation and annihilation operators are idempotent: .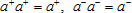

A sequential application of several creation/annihilation operators will produce many-element sets:

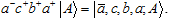
The order of operation may be quite significant, and it is only in very special cases that the set 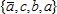can be identified with the set {c, b}.

With quantum elements "interfering" inside a set (however this interference is implemented), the state |a; A⟩ can no longer be understood as |a⟩|A⟩. Some very simple sets can be formed as products of one-element sets (the eigenstates of a particular operator); such states (and their non-degenerate combinations) are called "pure". Given a "complete" basis, we can "enumerate" the elements of the incident set:

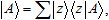
so that

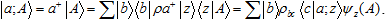
In this way, addition of an element to a general set can be reduced to a union of two-element sets: the new element a is to be sequentially coupled with each of the members of the base set. This obviously corresponds to the similar expansion in the traditional set theory:

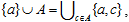
though quantum theory also demands accounting for interfering modes of virtual transition from one state to another.

Since we relate creation and annihilation operators to elements rather than sets, the union of two arbitrary sets is not always definable. Still, when the two sets have been produced starting from the same incident set (the "base", or "vacuum"), there is an option of considering the composition of the corresponding production operators as production of the union. This might be compared to the atomic states with different degrees of ionization. For yet another analogy, take the production of natural numbers with the only fundamental operation, the increment; the sum of two natural numbers is already an expansion of the original theory: this binary operation is imported from outside, being defined on a different level as a class of isomorphisms.

In certain cases, it is possible to define the union for the sets produced from difference base sets; this corresponds to the transition form atomic to molecular physics, with only the "valent" electrons and holes participating in the formation of the whole, while the atomic (ionic) cores are treated as relatively independent of each other (that is, the vacuum for the union equals the product of the original base states). Numerous options are possible, here too. Thus, one could compare the classical union as an analog of the covalent bond, with all the electrons equally belonging to each of the atoms in the molecule. In the opposite case, we obtain something like ionic bond, when the elements of one set get compensated by the holes in another. There is also an analog of the hydrogen bond, with no real union, but rather an "artefact" of the usage of a common basis.

The generalization of finite sets expansions onto infinite (countable or not) constructs is rather straightforward. From the practical viewpoint, it means considering a higher level, reflexive activity: instead of performing individual operations, we start constructing those operations using a regular approach. Like any hierarchy, set production can be folded into a "point", and then unfolded into a different hierarchical structure.

All the possible "interactions" between sets (set-theoretic operations and relations) are expressible through the combinations of creation and annihilation operators. Every special theory involves a specific collection of fundamental (elementary) interactions, so that the rest of the theory could be deduced from this axiomatic core. Since we are to eventually obtain a quite definite product, we reduce the result of each operation to the same reference basis; that is, the different combinations of elementary operations (the sequences of interactions) may lead to the same (in the sense of practical indistinguishability) set, while the interference of such virtual processes is reflected in the specific overall structure (spectrum) of the resulting set, up to the impossibility to obtain certain sets from the base (which is known in physics as selection rules).

This is the high time to ponder a little on the meaning of set comparison. What does in really mean, "to be the same"? The equality of elements is an entirely practical issue, it is determined by the organization of the object area. As for the equality of sets, opinions differ. It is usually said that two finite sets are equal if, and only if they contain the same elements. However, even that intuitively appealing definition is implicitly based on very thick assumptions about the object area and the sampling procedure (starting from the very possibility of enumeration). The situation is much worse with infinite sets, where we need to enumerate the elements of the both sets and compare them to each other in a finite (or even infinitesimal) time. Once again, quantum physics readily comes to mind, with the finer details of interaction "packed" in a single macroscopic point (or a moment of time), with the only observable outcome of a statistical distribution, a spectrum. Still, a similar sheme is possible in classical theory as well: consider one of the sets as a kind of a filter, a barrier, with the incident flow of the other set's elements that can be absorbed (or reflected) by the similar elements of the filter set; if there is nothing on the other side of the barrier (no outcoming elements), one can state that the incident set is less than the filter set (hence being its subset). Reverting the situation, with the incident set and the filter interchanged, we test the inverse relation: is there is still no output, the two sets are equal.

Obviously, this mental experiment is only one of the possibilities; however, it is enough to comprehend the idea of set comparison as a synopsis of numerous assumption about the character of interaction and the principles of dynamics. Just change the experimental setup, and you may get an entirely different picture. Well, there is nothing really new: for instance, there are different mathematical definitions of dimension, and we need to investigate the range of their compatibility. Similarly, with very large sets, we speak about their equinumerosity (or, at best, isomorphism) rather than true equality. Still, every man of reason would perfectly distinguish the sounds of speech from the graphic signs denoting them in the international phonetic alphabet: one can never convert one into another; the two sets are interrelated but not equal. In the same manner, even natural numbers are not the same as odd numbers, despite the fact that the two sets can be entirely mapped onto each other. The same score can be played with a violin, a piano, or an organ; but these instruments are in no way "isomorphic" in an orchestra.

The quantum paradigm brings in certain amendments, adding a "built-in" uncertainty, "partial" membership. With all that, the procedure of "filtering" one set with another is perfectly reproducible in quantum set theory; moreover, the transformation of a set into a filter here becomes a simple formal trick: all the element creation operators for one of the set must be replaced with the corresponding annihilation operators. As the resulting "holes" ("anti-elements") annihilate with the elements of the incident set, we immediately get the spectrum of differences in the end. That is, for the sets

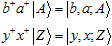
the result of their comparison is given by the amplitude

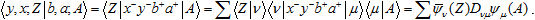
Under certain conditions, given the equality of elements a = x, b = y, this expression will evaluate to ⟨Z|A⟩, which is unity for equal base sets. Of course, in more complex constructions, such reduction to unity will not guarantee the complete equality of sets; however, if the virtual transitions can compensate each other to that extent, this means that one of the sets cab be effectively transformed into another, and hence be its fair replacement in a practical sense. Considering this expression as a function of some "macroscopic" parameters, one gets a full-fledged spectrum, where any virtual compensations will reveal themselves as structural peculiarities (e.g. resonances).

Quantum set theory does not just extend classical theory; it eventually suggests a bunch of specific implementations suitable for particular purposes. Similarly, in physics, any "theories of everything" admit numerous observable "landscapes". The choice is never arbitrary; our practical needs will select the acceptable solutions. Such practically-oriented mathematics will no longer be a mere play of thought: it will become sensible and truly meaningful.

Nov 1985