Global Relativity and Relative Locality
In the popular literature, it is often indicated that a relativistic observer is local. However, for a philosophically minded person, this is a rather strange kind of locality. Thus, we are said that measuring distances requires determination of two spatial positions at the same time, while time intervals are only meaningful in the same spatial point. To be sincere, this is a logical circularity, an implicit manner to postulate the invariance of the interval.
Physically, to consider two spatial points "at the same time", the observer must be much larger than the distance between the points, so that their separation would seem practically infinitesimal. Similarly, to take two instances of time "in the same point", we need to assume that the duration thus measured is practically negligible; otherwise, it would at least some motion within the instrument and hence spatial displacement. The orders of infinity must be correlated in a very special way, to achieve the desired result, which results in yet another logical circularity.
In these circumstances, a formal axiomatic introduction of relativity seems to be more consistent, albeit lacking physical justification. Relativism thus becomes an ad hoc construction; but is it much different from any other physical theory?
Well, what's wrong with the assumption that we can measure time locally, in the same spatial point? For a local observer, measuring distances will then require a travel from one spatial point to another; of course, the observer does not need to travel in person, as one can send and receive signals. This innocent statement contains an inner contradiction, as it takes for granted the possibility of probing signals of a negligible energy, so that they would not much influence the motion of the physical bodies and the state of the observer; however, small energy transfers mean large durations (both in quantum and classical mechanics), which may violate the locality of time measurement.
Here is the cheat trick. Travelling in person, we make our frame of reference essentially non-inertial, as we need to undergo some accelerations to start travel and turn back (to measure the local duration of the travel). In exactly the same way, a beam of light can be treated as an organ of observer that must be manipulated to reach the target and return to the starting point. For instance, a photon might be simply reflected by the target, to run back to the origin; but this necessarily involves momentum transfer, and hence the presence of physical forces. One could invent all kinds of intricate arrangements to circumvent the reflection scheme. Imagine an active media that sends a photon to the observer every time the object of interest (a probing photon) passes each spatial point. In this case, one could believe that there is no energy loss, and no deflecting forces. However, the very act of triggering the emission of the tracking signal by the medium requires a kind of interaction between the probing photon and the medium, just to make its passage noticeable. This is equivalent to photon absorption and re-emission, which means non-inertial behavior anyway, nothing to say about the inevitable time delays. Add here the energy cost of detecting photons in the origin point, where the observer must interact with the probing particle to determine its parameters relevant to the act of measurement.
Physics is an art of approximation. In real life, we can indeed stage certain kinds of experiments assuming the non-perturbing nature of measurement. Thus, in classical mechanics, the usual energy transfers due to the act of measurement are much smaller than the energetic scale of the physical process to study. However, today, we know it for certain that this approach does not directly work in many cases of interest. For instance, microscopic particles (as well as highly correlated macroscopic systems) feel any measurement as destructive and essentially changing their state (or the state of motion). This could be compared to a superheated liquid (or an overcooled gas) that would burst at any fluctuation. We avoid this difficulty restricting the nature of measurement, limiting ourselves to the asymptotic region far from the physical interaction zone. In this region, we presumably can destroy the outgoing particles without any considerable effect on the interaction history.
There are strong reasons for the region of very high velocities to be yet another problematic case. In our relativistic vision, any energy transfer (or the effective mass of the interaction carrier) increases with approaching the light barrier, so that no probing interaction could be considered as negligible. In terms of general relativity, this also means the presence of a mass that essentially distorts the geometry of space-time and makes motion non-inertial. That is, for very high speeds, no measurement can be considered as non-disturbing, and the overall scheme of special relativity theory fails. Since general relativity is postulated to be locally the same, its applicability near the light barrier limit is as questionable. Thus, popular physical theories undermine their own foundations, and it is a matter of sheer luck that they happen to be largely practical.
Still, let us imagine an idealized case of an observer (a physical system) who would be able to determine local time and operate with probing signals somehow avoiding such delicate issues. How could spatial distances be measured within a frame of that kind? For a spatial segment (a very rigid rod) at rest, we could sit at its center and emit photons towards the both ends. Registering the time needed for reflected photons to return to the origin, we multiply it by the speed of light (which is presumably the same regardless of anything) and thus calculate the distances. In this symmetric case, we effectively (or admittedly) apply the ruler simultaneously at the both ends of the segment, by the very setup of this mental experiment.
Now, let the segment move with a constant velocity along the axis. In this case, sitting in the origin, and emitting the probing photons at t = 0, we receive the reflected signals at different instances of time separated by a measurable duration Δt. It looks like that, if we knew the length of the segment, we could (with certain "natural" assumptions) derive its velocity in this reference frame from experimental data. Conversely, knowing the rod's velocity, we can derive its length (relative to the static observer). But there is no way to determine the both from the same measurement. A very familiar situation, isn't it? Quantum mechanical indeterminacy thus shows up in classical motion once again.
The situation gets even worse, as we can never be sure that the temporal discrepancy we detect has not been produced by a mere lack of symmetry, an initial displacement of the segment relative to the static observer. A rod at rest shifted along the X-axis can produce exactly the same Δt as a moving spatial segment. Moreover, receiving the reflected signals at the same time, we could as well assume the motion of an originally displaced segment, so that the two kinds of temporal discrepancy just cancel out. There is no way to distinguish spatial asymmetry from non-zero velocity in this experimental setup, which is yet another aspect of the intrinsic interdependence of space and motion.
As a result, the principle of locality is violated in such measurements anyway, since we can never guarantee that we are not comparing the distances from the observer taken at different instances of time. Once again, there is an implicit introduction of a global frame covering all the physical events of interest, so that the whole sequences of such events could be treated in a structural way, as coexistent at any moment (of a higher level). In experimental physics, data aggregation is universally popular, starting from mere statistical estimates, and up to complicated digital processing. All such procedures are obviously inconsistent from the formal viewpoint, but their practical acceptability speaks in favor of the idea of an essentially nonlocal character of nature, as reflected in physical science.
For example, take the same scheme of "radar" measurement to determine the position of a point by the time delay between the emission of the probing signal and the reception of the reflected signal. The very consideration of a point out there, away from the observer, is already nonlocal, since it assumes a finite distance present at any single moment; regardless of any quantitative estimates. Further, we take for granted that the point is moving relative to the observer and hence yet another nonlocal idea, a trajectory (possibly contracted to a single point) described by the parametric equation
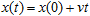 . .
Similarly, the trajectory of the probing signal is a nonlocal entity described by the equation
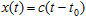 . .
At some tx the two trajectories intersect (if ever), and the reflected signal travels back to the observer (in the assumption of the constancy of the speed of light) along the trajectory
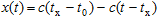 , ,
to arrive to the origin at
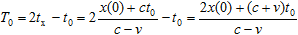 . .
Since there are two unknown parameters, x(0) and v, we cannot tell much from a single measurement. Now, if the next probing signal is emitted at t1 = t0 + τ, we get
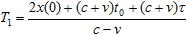 , ,
and the velocity of the moving particle is readily evaluated from aggregated measurements:
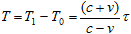 , ,
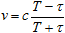 . .
Obviously, by construction, thus measured speed of the point will always be less than the speed of light (otherwise, the intersection of the trajectories would become problematic).
A similar version of this technique would employ the registration of light emitted by the moving source rather than probing signals. This modification is extremely popular in astronomy, where most information about the motion of the deep space objects comes from Doppler shift measurements. However, in this case, we do not know the exact period (wavelength) of the emitted signals, and we need to adopt additional assumptions about the physical nature of the emitting system. Thus, we must be sure that the frequency of the emitted light does not depend on the kinematic and dynamic conditions, or introduce the appropriate corrections where such dependence might be important (like in the case of the "transversal" Doppler effect due to relativistic time dilation).
This is how formal manipulations help us to "extract" physical information from measurable quantities. Sometimes, it may be difficult to convincingly draw a distinction between "extraction" and "introduction". No theory can justify such tricks; it is the practical applicability that always has the final word. Just imagine a different kind of nature, a nonlinear world, where the distances do not add up in the usual way, so that the sum of two lengths x1 and x2 would be given by a nontrivial function:
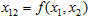 . .
Similarly, the definition of velocity may as well be nonlinear:
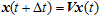 , ,
where V is a nonlinear (and possibly nonlocal) operator acting on the position vector (which can be no vector at all, with the addition law as above). All the logic of measurement is then to be revised, to produce quite different estimates. Of course, we respect the correspondence principle; but the correct asymptotic behavior can be achieved in an infinity of ways. The typical problem of overextrapolation is due to the common illusion about the abstract nature of mathematics apparently independent of the application area. However, the admissibility of that particular kind of mathematics, or any other, is a practical question, a decision to take, which is of primary importance in the development of any theory. If we add one quantity to another, we must be sure that these quantities could naturally sum up, so that the very operation of addition would have a practical implementation. That is, the formalism of a science is closely related to the ways of action; in particular, any meaningful theoretical result must be interpretable in material terms. For instance, when we formally solve an equation via a suitable variable substitution (in the parametric form), we employ the knowledge of the physical symmetries that are really present in the system and reflected in the structure of the original equation. Treating them as purely formal, we only indicate that they are not yet of interest for the present study, but this does not mean that they could not come forth in a different context.
Returning to the issues of (non)locality, we must conclude that, in any measurement, there is a local model of a nonlocal world, and we use that model to map the observable events. We admit that the resulting picture reflects the structure of the real world out there. That is, using our (presumed) knowledge of the world's dynamics, we can restore its state at any instant as long as causality prevails over stochastic features. This state is absolutely nonlocal, but, in this sense, it is certainly measurable. The logical contradiction is complete: the assumption of locality leads to a nonlocal view of the world.
A stubborn physicist would proceed inventing all kinds of conceptual appliances to eliminate nonlocal dynamics from fundamental science. From the philosophical viewpoint, it is evident that all such inherently fallacious attempts will eventually get stuck in contradictions. There is the only world, and everything that happens belongs to the same Universe. The very separation of an individual thing from the rest of the world means that the thing's environment becomes as definite and hence can be reflected in (represented by) that very thing. The degree of the "inner" and "outer" definiteness is exactly the same. That is, every local feature will have a global counterpart, and no physical description is possible without a good portion of nonlocality. As there is no way to drive it out, it's not worth the effort and we'd better occupy ourselves with the problem of control. Once consciously admitted and recognized, the level of nonlocality is a perfect indicator of the scope of the model.
As everybody knows, nonlocal behavior is basically related to the formation of compound systems incorporating many local components. The characteristics of collective behavior depend on the lower-level motion in a nonlinear manner, and this makes the adjacent levels of hierarchy qualitatively different. Take the simplest case, the purely mechanical motion of a number of material points with a central interaction (an obvious source of nonlocality). Two bodies rotating around a common center of mass is a typical example of a compound system, and the traditional approach separates its inner motion from the motion of the center of mass representing the overall motion with a linear combination of the corresponding position and velocity vectors. However, this linearity gets broken as soon it comes to any additional interactions. The compound system will only interact as a whole with the bodies far away from the position of the center of mass; that is, for distances much greater than the typical diameter of the couple, and on the time scale much slower than the rotation period. Moreover, even without any other bodies, the very act of observation puts the whole system in a spatial and temporal context imposing an "artificial" structure on the measurement results. Thus, for a "localized" observer with an observation window much smaller than the inner motion scale and the registration period much less than the period of rotation, the motion will be apparently stochastic, while an infinitely large (adiabatic) observer will see a single point moving in an empty space; of course there is a whole range of intermediate cases. A numerical simulation for a simple 2D oscillator provides an illustration of this "imposed" pattern formation due to a limited field of view (see the figure below).

In this line, we must admit that the unity of the world means a universal nonlinear entanglement of all the things and events, and any physical structure is to be unfolded in accordance with the structure of the current activity. As a result, the hierarchy of human activities determines a hierarchical vision of the physical world. A frame of reference is, in general, an instance of such a hierarchy.
Now, we come to the problem of comparing different frames. Formally, one needs a hierarchy of frames, so that the frames to compare could be placed together within the same higher-level frame. Objectively, this assumes a common activity, with the same object and product for a number of active subjects (which, of course, do not need to be mere individuals). Taking physical experimenting for a class of such reference activities, the only way to compare different observers is to make them report on the same physical process. This task is not as trivial as it may seem. It requires, at least, a certain idea of "sameness". The two observers must agree on a range of physical events they can see together. Thus, if some event takes place for one observer, but is absent for the other, there is simply nothing to compare. On the other hand, to be comparable, the common events must be viewed from the same angle. If one observer is interested in the body's trajectory and the other in its temperature, they have no news to exchange. In view of the abovementioned duality of length and speed, one could also doubt the possibility of comparing the qualitatively different (complementary) aspects of the same. Thus, a moving observer can certainly determine a rod's length, in its own frame of reference where the rod is at rest. The static observer could take the length thus reported for the reference in the velocity measurement scheme, as above. In this case, two complementary measurements would be enough to completely specify the state of the physical system. As the relativistic theory suggests, this is not so. That is, aggregating data from different sources is a risky operation that may produce spurious results.
This problem has long since haunted the science of astronomy, which often deals with slow processes to trace over many decades, or even centuries. Astronomical observations are known to depend on many factors, and the method of raw data processing is of crucial importance. Astronomers have developed intricate protocols of reporting, which allow to adjust a huge bulk of earlier observations to a newer value of some basic parameter, thus introducing the necessary corrections without the need of overall revision. Of course, there are influences that cannot be formally fixed; nevertheless, much of the relative movements of the celestial bodies can be kept as a trustable evidence. However, for an extraterrestrial observer, such a detailed account might be of no value unless there is an objective procedure relating one reference frame to another.
We can never tell for sure how the others see the world. We may trust their observations, but their reports picture the world from an unknown perspective. Any comparison requires a number of strong assumptions, reflecting our ideas about the way we act as well as the way the others react. But here is where science ends. At any instance, we perceive the world but not our own perception. The observation of the way of observation is a different kind of observation. As soon as we try to incorporate reflection in physics, we come to a complicated non-deterministic (if not mystical) picture. Still, everybody knows that science is possible, and that it can be very efficient. Why?
Once again, the answer is practical. Any science studies some portion of reality inasmuch it has already become an object of a common activity. All the preceding experience that has eventually led to establishing such a commonality is outside science. All kinds of methodological considerations used to "scientifically" extrapolate the past experience into the future are outside science either. It is no use to ask a physicist to explain physics; physicists do physics, and they should (and would) rather ask somebody else if they ever needed any explanation. To compare the frames of reference, physicists employ the commonality of physical events that has been practically established. In other words, they do not admit anything—they only act as admitted. This is the primary nonlocality built in any physical theory.
When it comes to the foundations of science, we are free to choose the level of consideration according to the current practical needs. That is, among the infinity of assumptions, one selects only those that are the most likely to vary, and the activity of systematization is only to provide a platform for further revision of the system; in reality, the fundamental principles are always formulated from the viewpoint of a (preliminarily) reformed theory.
Like in any hierarchy, the structure of a science is mutable, subject to hierarchical conversion. Even within a very limited task, the substantiation of the principle of relativity, there are multiple choices, and different opinions may equally go. Thus, inertial frames of reference were once preferred as avoiding "non-physical" forces and clearly indicating the "basic" dynamics; any accelerated systems were treated as auxiliary and purely technical means. However, since there are no interaction-free systems in the real world, the notion of an inertial frame of reference has gradually evolved to an abstract idea, while any real frames should necessarily contain some kinds of "fictitious" forces due to the complex character of the motion of the references frame. As long as we hold to a local description, there is no way to tell a "spurious" effect from a "physical" interaction, since neither frame is preferable in an absolute sense, and one can only speak about the classes of dynamically similar frames interrelated by "inertial" transitions in a general sense, not restricting ourselves to the constancy of the relative velocity. The different classes of "inertial" transitions are characterized by their key invariants. For example, the laws of mechanics take the same form in all the frames moving with a constant velocity relative to each other, which is the most commonly known kind of inertial motion. However, if we consider the total energy (or an equivalent temperature) as an essential physical parameter and hence a required invariant, such uniform translations can no longer be considered as "inertial", as they mean an increase of the kinetic energy due to the motion of the system as a whole.
It is not quite clear, whether the criteria of inertial motion may include various statistical characteristics. Such parameters are often dynamically asymmetric, so that the transition from one frame to another cannot be "undone" by the inverse transition. Still, non-commuting operators have long since become a habitual feature of quantum field theories, and the constructs like temperature or pressure field do not much differ from a distribution of masses or electric potential. In a way, any physical quantity at all is statistical, as any physical notion (like any notion at all) refers to a class of the possible "microscopic" implementations rather than a unique pure state. With all that, the meaning of relativity remains disputable. Is it physically acceptable that the body's temperature in one frame of reference raised while falling in another frame? And what about the entropy? Cain killed Abel—or maybe the other way round?
However uncomfortable, the ghost of universal mutability is going to haunt science in any realm and for all times. This is the price we pay for deliberate locality. Even admitting a kind of global criterion to sort out our current impressions, we do not exorcize the evil, since the very distinction of the lower and higher levels in a hierarchy is limited to a specific conversion, a particular unfolding. The behavior of a crystal depends on the properties of the atoms and molecules; however, the atoms and molecules in a crystal behave differently from the same atoms and molecules in a fluid or a plasma flare. A brain of an animal is functionally different from the brain of a social animal, with the identic physiology. Similarly, the local motion of a material point in a given frame of reference could as well be considered as a manifestation of the very way the reference frame is constructed and introduced.
So, let's take it easy and never care much about any exhaustive explanations. The predictions of science should be treated with a grain of humor. There is no reason to get scared by our own imagination. Science is great at suggesting us plausible ideas of what could be done. But these ideas remain sheer abstractions until somebody really does it (often in a way very different from the originally predicted). And, of course, no science can prevent us from doing "wonders", however impossible they might seem from the scientific viewpoint. A new science will come and lift traditional restrictions. We cannot tell in advance, which impossible things are to become possible in the nearest future; but we may be quite certain to get some, and so without end.
Yes, in real life, one cannot live by mere wonders. Otherwise, they would not indeed be wonders. This is the same issue of the local eggs from a global hen. As soon as we get a workable solution for a class of practical problems, we'll do our best to develop the relevant science within the chosen conceptual framework (which is a kind of reference frame too). Virtually, this is the only way to reach the limits of its applicability, where we could start exercising our magic power once again. Meanwhile, philosophy is just a funny toy and a source of consolation when a problem turns out to be really hard. So, once again, what can be said about our local dwellers of a mechanical world, with their clocks and lightning probes?
The model of a reference frame assumes that different observers are all "embedded" in a higher-level formation distinguishing them by a set of global parameters (for instance, relative velocities). One could argue that these velocities are not really global, as they are measured by one of the observers and hence depend on the current (local) frame. However, the principle of relativity suggests that the observer "1" moving in some reference frame "0" will see exactly the same picture, with "0" moving with exactly the same relative speed in the opposite direction. This symmetry is treated as an important physical feature, but it does not follow from any local considerations.
Further, each observer is deemed to have the complete information on whatever happens in his own frame of reference at any instant; that is, a local observer is absolutely global within the rest frame. This is a very strong assumption, but it is always implicitly made. Basically, this means that a reference frame is something quite definite, an instant structure tractable as a whole. This, again, puts a reference frame in a higher-level context, making it a point in a global sense.
Since comparison of reference frames is primarily a higher-level operation, the corresponding observers do not need to be aware of each other and of their relative motion. The interrelation between the different frames of reference is therefore objective. Nevertheless, nothing prevents a local observer to interpret a moving object as another observer and picture the world from that hypothetical observer's viewpoint. This subjective (local) relation may differ from the objective law, as the lower level structure does not immediately reproduce the peculiarities of a higher level. Local comparison is, in fact, a three-step procedure: first, we guess for the global representation of the both frames, then we compare them in an objective way, and finally, we need to project the result back into the local frame. In physics, we often forget about the first and third stages and treat our local theories as objective laws "discovered" in (and "confirmed" by) the empirical data. Note, once again, that (re)constructing another observer's view of the world is different from the local description of that world; these are quite different activities, and the possible correspondence between them cannot be explained by any local considerations.
It seems natural to stick to the same structure of the reference frames for all the observers. As one observer cannot immediately see the world by the eyes of another, one is bound to use one's own ideas to express what the others might fancy. In other words, we make the observers clones of each other, acting in the same manner and representing the results in the same abstract forms. However, such a universality is yet another global feature, and, in general, this requirement could be weakened on a higher level. On the other hand, an apparent local discrepancy between the reference frames may be (at least partially) spurious, resulting from the transitions from the local to the global description and back, with much simpler inter-frame relations on the global level. For instance, on a higher level, the equations of motion could be exactly the same for different observers, while taking a much more complicated form in the local frame of each observer, involving a number of "inertial" forces. The same structure of the local reference frames would only mean a regular relation to the higher level. On the other hand, due to hierarchical conversion, the very distinction between the "horizontal" and "vertical" relations in a hierarchy is relative, and the procedures of folding and unfolding the hierarchy are not unique. The identity of the frames of reference is, therefore, to select a consistent hierarchy of hierarchical structures.
It is an open question, whether physical space and time could be treated in a global manner on some level, while remaining relativistically entangled in local observations. The correspondence principle and the traditional asymmetry of spatial and temporal dimensionality speak in favor of such an idea. Yet another indication of the same could be recognized in the instances of "hidden" relativism, when certain properties of a classical (macroscopic) system can only be explained by some inner (quantum) relativistic effects. That is, to produce an observable picture in a local reference frame, we need to transform the higher-level (global) space and time selecting one of the possible rules; the collection of such rules represents a physical symmetry, which does not necessarily depend on the relative motion of observers. Since each observer can independently vary the parameters of the symmetry group, the pictures of motion in different frames are not necessarily correlated. The transforms of special relativity result in a very special case of "cloned" frames, related to each other through some global parameter. This closely resembles the idea of "quantum entanglement", in purely classical motion. Conversely, the explanation of quantum correlations could be related to a layered nature of motion.
Just to conclude, let us ponder a little over a few potentially problematic issues in comparison of reference frames. For instance, a typical illustration of special relativity compares the observation of the motion of a spatial segment (a rigid rod) by two observers (inertially) moving relative to each other. If the rod is at rest for one of the observers, we conjecture that the other would see it as moving with a (presumably) constant speed.
In this setup, the very idea of an extended body violates strict locality. To perceive the rod as a whole, both observers must somehow learn about its existence and identify its two ends with the same object, then agree on that the two observers speak about the same thing… Quite a program for a local observer, who (ideally) does not see anything beyond his own location and who cannot measure but time delays. Still, scientists are most resourceful to do things like that. Otherwise, we would know nothing about far Universe, where our spacecraft has not yet arrived. As well as about the microscopic world, where we'll never arrive. Practically, this requires a series of independent measurements along with an intricate interpretation procedure based on some general theoretical picture. In our mental experiment, we have to assume that all the preliminaries are over, and the vision of a space segment as a physical object is given to the both observers "by construction".
Still, the possibility of any common events remains questionable. Thus, admitting that both observers use the same probing signals to arrange the points of their reference frames, we cannot be sure that they do it in the same way, unless one observer could directly observe the procedure of measurement as performed by the other. That is, we have to compare the very acts of observation along with the resulting relative pictures of motion, which obviously gets us back to the hierarchical vision of a reference frame. However, in reality, we rarely observe the very propagation of light (though, theoretically, it can be made visible, in some very special media). Of course, we do not mean various phase effects, like the visible motion of a shadow, or the march of the dawn over the globe. Normally, we only detect light emission and absorption, which are the natural candidates to the collection of comparable physical events. With all that, using strictly collimated light signals (narrow beams), one observer would miss a signal sent by another observer in the opposite direction, and the commonality of the probing signals would be ruined. To override this difficulty, we could assume that probing signals are spherical waves, and they can be detected at any angle. In a mental experiment, we do not care for the practical feasibility; in real life, the limit cases of extremely weak and extremely strong signals could raise questions about the applicability of the approach. Of course, a wave (and a spherical wave in particular) is an essentially nonlocal entity, smelling the confusion of a classical and a quantum description once again. From the logical viewpoint, we implicitly introduce a very strong assumption that any reference frame occupies the whole physical space (while remaining an inner space of the observer). In this global relativity, we can catch any signals regardless of the direction of emission; somehow thus obtained information becomes attributed to the same spatial point (the location of the observer), making it local (and hence relative). The same logical background is to cope with the influence of the hypothetical faster-than-light motion on the range of common observations.
A complementary logical issue is brought about by the idea of a spatial direction. How can we determine directions locally, in a point? Even with infinitesimal displacements, we need to leave this point and get back. A vector thus becomes an abstraction of a cyclic path, a very special case of nonlocality. On the other hand, time measurement is wholly based on comparison of cyclic processes; a typical clock is an essentially nonlocal spatial device, and we always decide on time using a spatial distribution. To isolate this nonlocality from the rest of the physical system (which could then be deemed to be local), one might employ dimensional separation, and hence the inherent nonlocality of spatial directions. In a way, the origin of the relativistically entangled space-time is due to the relative nature of spatial orthogonality.
Considering light emission and absorption (sending and receiving signals), we come across yet another problem. How can we know that the photon we receive here and now has come from a faraway object that has sent it long ago? This is an essentially global idea that does not follow from any local measurements. As all photons are like each other, there is a risk to confuse one object with another, and get a distorted picture of reality. In practice, such issues are resolved by repeated and prolonged observation; if they reproduce approximately the same picture from one measurement to another, we conclude about the existence of some outer objects that produce the observable effect. No scientific notion (and virtually no notion at all) refers to an individual measurement; we first obtain an overall picture and then extract the details of interest as the qualitative feature of the whole. Of course, such averaged pictures can eliminate important physical effects and introduce spurious dependencies. To check their validity, we need to compare data from many independent sources employing alternative physical mechanisms. The simple scheme of cloned observers using the same measurement techniques to obtain the same global structures (reference frames) is therefore physically meaningless, or, at least, heavily restricted. To put it otherwise, a frame of reference is a kind of collective effect, with many nonlinear (global) interactions resulting in a relatively stable formation on a higher level of hierarchy.
|