Nonlinear Kinematics

The traditional Newtonian mechanics was a formal expression of the early human experience of motion, which was desperately sluggish by modern criteria, even in the common urban activities, far from relativistic speeds. Similarly, the experience of size and time grew from the compact things and finite events of everyday life, boldly extrapolated onto much longer distances and times. The vision of the physical world was largely anthropocentric, as people were primarily interested in what happened in the nearest neighborhood. Hence the essential linearity of the first quantitative estimates and the taste for extensive measures, piling up many little bits to get a big thing of the same kind. Everybody knew that, applying a ruler twice, we should get a distance twice as long, and turning a sandglass twice would mark the doubled waiting time. The first physical notion of space took it for an infinite sum of tiny rulers; the incommensurability of lengths that was quite a challenge for a formal mathematician did not much bother a physicist, as physical "points" could be rather large, remaining "infinitesimal" compared to the regular lengths of the model. Any differences within the typical experimental scatter could be realistically ignored. Similarly, a physicist may speak about infinitely small volumes in a gas, meaning that each volume still contains a huge number of molecules, to remain a thermodynamic system. Similarly, time was deemed to be a chain of elementary duration small enough to label physical events to the accuracy of the clock. In this "flat" physics, it was natural to characterize mechanical motion by the number of space units covered in a few units of time (velocity), and the total length of the path could be obtained as a sum of "infinitesimal" lengths spanned by the moving body in a single unit of time. Physical interactions (forces) might change the speed, but these changes still happened on a scale much below the accuracy of measurement and could be treated as independent of spatial displacement, pushed to yet lower level (which obviously puts an upper limit on the admissible speeds). The independence of the different levels of motion and the possibility of their superposition was yet another manifestation of the model's linearity.

The power of this simple picture was the other side of its primary conceptual weakness: the observable behavior of the system was tied to the (physical) scale. For instance, a periodic process represented by a smooth curve will show up as chaotic motion on the time scale much courser than the process' period; in some scales, the same process may look like a stationary state (a point, several points, or a spatial form, a body). The very consideration of different scales violates linearity, while any linearity at all is impossible without combining very different levels in the same theory. In this sense, binding time to space and considering curved space-time was a logical completion of that line. And a physical conclusion too, since relativistic time dilation and length contraction are bound to eventually violate the condition of the physical separation of the different levels in the linear model. The new physics is to investigate the virgin lands beyond the principle of superposition.

Just for illustration, let us keep within the smooth world of Newtonian mechanics, but admit that the transition from of spatial point to another is a little more complex than mere additive displacement. Traditionally, we write:

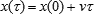
This expression unequivocally hints to the infinitesimality of spatial displacements due to the proper motion of the system as compared to the range of movements required to build the coordinate system (a frame of reference):

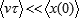
That is, both velocity and time must be small enough. Trying to compensate long durations with very slow motion or, conversely, very high speeds with microscopic time, would mean yet another instance of level separation, and hence a retreat from physical uniformity. In some situations, this is a legal approach. Infinitely slow changes obviously corresponds to the usual adiabatic limit, while the opposite case of instantaneous transitions in an inner space drives us to a kind of quantum description. However, the both opposites imply an essentially nonlinear procedure of interfacing two levels of hierarchy with very different character of motion. This is normally achieved using a kind of statistics.

In the simplest case, one could add nonlinearity through an additional term quadratic in time:

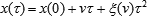
which (for bounded v and ξ) seems to merely account for acceleration; but here, we mean a purely kinematic rule, and there is no physical force responsible for the effect. In some cases, this type of nonlinearity can be locally represented by an effective force; but this identification is in no way justified when it comes to the global structure of space-time. Thus, postulating the equivalence of a physical interaction and the spurious forces due to the non-inertial motion of the observer, we extrapolate a local observation onto the whole Universe, which is a logical fallacy. The above nonlinear displacement formula physically means that local geometry may change with time; for quick events, this effect is negligible, though it may become significant on the cosmological scale. Moreover, for a very long τ, the linear term is utterly unimportant:

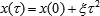
which may also refer to the stationary systems (v = 0) exhibiting a kind of "cosmological" fluctuations. One could consider this addition law as the opposite to the usual diffusion formula, with the distance proportional to the square root of time.

Alternatively, one could admit the orthogonality of kinematics on the different levels of hierarchy:

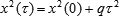
which, in certain cases, could be approximated with

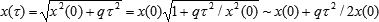
thus returning to the same quadratic nonlinearity, with the only difference that the "cosmological" admixture depends on distance (which might be physically attractive). Of course, there are many more possibilities, neither of them being preferable from the formal viewpoint. Any choice comes from practical reasons. Still, the awareness of the very possibility of different kinematic frameworks is a remedy against mental stagnation and the exaggeration of the universal significance of the present state of our knowledge.