Observers, Time, and Velocity Measurements

Today, everybody knows that the speed of light does not depend on the motion of the source and that it is the same in any frame of reference. This fact has been confirmed by very accurate measurements; it is also supported by the overall consistency and impressive progress of modern physics entirely based on this assumption. As a consequence of this picture, we cannot move faster than light, and our ideas about space and time have to reflect their interdependence albeit leading to uncomfortable differences in the picture of reality for different observers. Of course, the classical picture of entirely separated space and time, the same for all observers, was simple and attractive. Nevertheless, science has to follow the turns of reality, however crazy they would seem to a primitive mind.

Still, one is always free to ask why. Thus, in the ancient times, people simply accepted the regular motion of the sun and the stars across the sky as a physical fact; this lead them to adjusting their measures of time to the observed regularity. The characteristic periods of this motion should be considered as fundamental constants, and this view was equally practical in both Ptolemaic and Copernican pictures of the world. Later, Sir Isaac Newton has explained us that all such regularities could be derived from a simple law of attraction that was named universal gravitation—just to denote something we do not yet understand. Some newer theories admit that the gravitational constant from Newton's law could be derived from a more general theory, along with a number of other fundamental values. There is no reason to take the speed of light for something special, and we could lump it to the same pile.

Historically, the relations between physics and reality provoked a lot of debate. It is quite obvious, that all our notions refer to the aspects of the world that have already been included in our practical activity, and we do not care for theories of something beyond any (at least speculative) accessibility. It is important that human activities are never confined to mere cognition; moreover, cognition is rather an auxiliary activity serving to our principal goal of rearranging the world to better satisfy our needs. Still, the essentially practical nature of cognition leads many thinkers to belief that there is nothing at all in the world beyond human activities, and that the whole nature must be treated as an artefact, the result of our active attitude to the world. In a way, they are right, as long as the present state of human development is concerned, regardless of its origin and the prospects of the future. However, when we consider developing activities, we need to think about the source of this development, unless we are apt to take the world for mere play of imagination. It would be quite natural to admit that the world is much wider than our present experience, and that is why we are always bound to get new, unexpected experiences in the future. This "world on itself" is not static, and therefore our experiences will grow not only through expansion assimilating the new parts and aspects of the Universe, but also in an intensive way, due to the development of the world itself. That is, we can never have a "complete" picture of the world; there will always be something to add, or something to change. Some would find it disappointing; some others would greet it as a source of infinite fun.

In particular, our ideas of space and time are necessarily dependent on the range of activities available at the moment. The earlier notions of space and time were different, developing from the patchwork of disjoint local environments to the classical mechanistic vision of space and time as static universals. When we bind these universal space and time together through the introduction of a universal constant, the speed of light, we reproduce, on a higher level, the primeval ideas of space measured by time, and time determined by the spatial positions of the visible objects. The obvious corollary is that a wider vision of this interdependence as a special case of a more universal picture will require at least one alternative "space-time" constructed on a different basis. In the developing world, the constancy of the speed of light could be a local phenomenon due either to the limited experience of our observations, or to the present state of the world's evolution. That is, even with the present technologies, one could expect detecting certain variations with time, or somewhere far away. Alternatively, one could admit that our relativistic space-time is an artefact of the present measurement schemes, and that new independent measurements would reveal considerable differences. As usual, any combination of the two possibilities is also possible.

As we cannot say anything meaningful about the unexpected, let us look closer at what we have at hand. The very idea of motion is nontrivial, since one has to consider two successive states of the system at once, relating them to each other as "previous" and "subsequent". But how can one compare two entities, of which one is already gone, while the other has not yet come? This assumes that there an entity comprising both the initial and final states, something that does not change with them and hence can serve as their common measure. That is, an entirely local observer existing here and now can never detect any motion, only registering the current state at the present moment. Indeed, even registering the current state becomes highly problematic, as there is no way to distinguish it from (and even to compare it to) any other state.

This argument seems to undermine the fundamental assumption lying in the basis of relativity theory, the locality of observations (interactions). It is usually said that any observer can only compare events occurring in the same spatial point. On the other hand, we admit that space and time are intertwined and inseparable; this implies that the notion of "the same spatial point" contradicts the overall covariance requiring a preferable frame of reference. Obviously, postulating a covariant locality embracing both space and time will eliminate any motion at all. This is one of the reasons for a purely geometrical vision of the world becoming so popular among theoreticians. The world, where nothing happens, where everything is already given and never subject to change… But the very idea of such a static world is an expression of extreme nonlocality expanding the observer to the whole space-time. Or, alternatively, the whole space-time is to be located within a single point-instant, that is, it must be the inner state of the absolutely local observer irrelevant to any outer motion.

To allow of any meaningful science, we have to adopt a hierarchical vision of locality, so that local outer motion (local interactions) are to be complemented with essentially nonlocal inner motion serving to distinguish outer events by associating them with the different inner states. That is, a local observer maps all the instances of interaction with the outer world into an inner space (taken at once, but possibly including a static counterpart of the temporal dimension). A structure thus obtained represents the outer world in this particular frame of reference.

Of course, nothing prevents us from considering more levels of hierarchy; moreover, this hierarchical structure does not need to be the same for the different aspects of the same physical system. The observer (and the frame of reference) will become hierarchical as well, being both local and nonlocal, in respect to different levels of hierarchy. In this general approach, locality is relative as anything else.

The natural organization of the outer events will induce hierarchical structures in the inner representation space. Obviously, these structures also depend on the way of mapping, which is virtually related to the currently available modes of activity. This is why the inner structures may be inadequate for the description of certain physical areas, reproducing them inside the observer in a cumbrous or ambiguous manner. However, our practical activity tends to bring our representations to a closer correspondence with the real world; in a self-reflective form, this is what we call cognition. Of course, in physics, we do not consider any conscious beings, and a physical observer is merely an equivalent name for a frame of reference associated with an individual physical object (real or virtual), provided it exists as a relatively stable formation distinguishable from the rest of the world. That is, we can speak about "observer objects" reflecting all the other objects; obviously, any other object can be chosen for an "observer", which will modify the observed picture in a regular manner determined by the physical nature of the observer objects (the level of "observation"). This generalized relativity holds for any physical systems at all, not necessarily of the same kind. The same physical world becomes reflected in a variety of relative physical pictures comparable with each other. For instance, the kinetic derivation of thermodynamic regularities could be considered as a shift of reference level within the same hierarchy. The notion of an inertial frame can be extended as well, referring to the frames of reference within the same level of hierarchy. In this case, the different observers will build essentially the same picture of the physical world, while any inter-level transitions require a different dynamics (like adding or elimination of interactions and symmetries).

Any outer motion imposes a definite type of structure on the inner space; namely, it produces trajectories (or tracks) representing the sequences of events. In general, a trajectory does not need to be smooth, without loops and self-intersections; moreover, it may be chaotic and fuzzy, so that a physical process would be represented by a bundle of trajectories rather than by a single track. Still, at any instance, there is a distinction of the present and the past: a part of the trajectory is said to occur before the current state, while the rest will represent the subsequent motion. This relation may also be nontrivial, reflecting the hierarchical organization of the "present moment". Anyway, a trajectory is a kind of hierarchical structure, with the present state lying "above" all the preceding states and "below" all the following (if the structure is to represent development, or evolution), or conversely, "below" all the past (when considered as unfolding the structure from some original state). This relativity of the past and the future is reflected in the common idea of the isotropy of the physical time.

Yet another aspect of time is related to the idea of homogeneity. Thus, a physical system (an observer) is not likely to imprint anything that did not yet happen, and hence the inner space of the observer might seem to be essentially finite, limited by the past experiences. Any trajectory in the representation space must break at the "present moment", so that all we have is the memories of the past. However, as soon as there is certain regularity (conveyed by the term "homogeneity"), we can shift the reference point to one of the previous instants, thus obtaining both the future and the past. A generalized view of homogeneity does not impose any restrictions on the character of motion; the only uniformity we need is the very ordering of events, so that one of them goes before another on the same trajectory regardless of the reference point. Now, for each past "point" on the track, we have some continuation, and there is no way to determine how long it will last as long as we consider only local experiences. A photon does not know that, a moment later, it will be absorbed by an atomic electron, and the present state of an electron does not imply any further change (or annihilation). In this sense, the homogeneity of time makes it locally infinite (extrapolated by homogeneity); of course, various "catastrophic" events (meaning the end of one track and the beginning of another) will violate homogeneity thus introducing relative finality of time. As all the objects in the world are finite, there is always some "end of time": real objects do not live forever, and the corresponding frames of reference are limited; however, in a local picture, each frame of reference is infinite in time. Formally, any singularity means a higher-level event, a transition from on local picture to another via a global view. The notion of homogeneity is obviously applicable to the spatial dimensions as well, with the same dialectics of infinity and singularities.

In general, a trajectory in the observer's inner space does not imply any measure of time; it is nothing but pure sequencing of events. However, the very presence of such an elementary hierarchical structure will also introduce the idea of transition from the previous state to the next, however adjacent. A transition does not belong to the same representation space, though it can sometimes be represented by an intermediate state. In other words, a transition is an element of a higher level, so that the state of outer motion becomes represented by a hierarchy of inner transitions. In the simplest case of the mechanical motion of a material point, one could picture it as the transition from one spatial point to another; such transitions can be represented by the vectors of displacement (lying in the tangent space). In quantum mechanics, we consider transitions between the points of a configuration space; quantum transitions are represented by special operators. Event tracks and transition sequences can often be considered as the dual representations of the same outer motion; however, this duality holds only in the regions of homogeneity, while the presence of singularities (global events) makes the two levels essentially different.

Now, a sequence of outer events is represented within the observer by a (static) track in the representation space (frame of reference). Due to homogeneity, all we know of time is local ordering, and there is no idea of duration, which must be essentially non-local, comparing at least two different points on the same trajectory. One could be tempted to associate duration with transitions, which are also connecting one position to another; however, this program won't work, since transitions only provide a kind of spatial measure (or distance), characterizing the difference of events rather than their temporal spread. The only way to introduce a measure of time is to compare one track with another serving as a clock. That is, we need yet another level of hierarchy allowing of a global view on separate sequences of physical events within the same reference frame.

When the events on some trajectory are associated with the events of the clock process, the distance between the reference events ("clock ticks") can serve as a measure of time elapsed between the events of the target sequence, providing a kind of duration. Comparing the distance between the events on the target track with the corresponding duration (the distance between the clock ticks), we obtain a measure of the rate of change; in particular, mechanical velocities can be defined in this way.

However, to efficiently serve as a clock, the reference process must run on a different level of hierarchy (a different time scale), thus ensuring the least interference with the events on the target track. Indeed, if the two sequences develop in parallel, one could treat a pair of events belonging to the target and clock trajectories as a compound event; physically, such parallelism means either the presence of a specific interaction coupling the two events together, or the presence of yet another level of hierarchy synchronizing the two sequences in a kind of collective behavior.

The very act of associating the events on a trajectory with the clock ticks means broken homogeneity. This additional interaction introduces a specific singularity, which, in general, will distort the physical picture. However, if the clock as a sequence of singularities is implemented on a different level of hierarchy, this distortion is equally present in any point on the target trajectory, and homogeneity becomes effectively restored.

The same frame of reference may be equipped with several clocks, assuming a number of different time measures. However, as long as they are associated with the same physical process, these measures will necessarily be coordinated. Still, nothing prevents the same observer from using independent time clocks for different physical processes, thus making them virtually incomparable.

Once again, in physics, we do not need to consider any conscious observers; it is physical processes that are compared to each other. Any temporal effects appear as the interference of different processes, providing the measure of time for each other. For strongly coupled processes, there is no time; temporal characteristics of a physical process are related to the presence of a weak interaction that does not much violate the overall picture.

Basically, the duration of a physical process can be evaluated as the number of clock ticks (acts of measurement) between the starting point and the end. Of course, for closely spaced clock ticks (in the limit of a continuous probing interaction), a corresponding density is to be used. From this perspective, the clock looks like a periodic process (though its period may be largely varying as measured by another clock). To allow such abstract counting, the individual ticks must be practically identical, while remaining well distinct as independent events in the clock process. This contradiction can be lifted in a hierarchical clock, with the lower-level cycles (the interval between the adjacent clock ticks) labeled by the phase of a higher-level cycle (a count), which, in its turn, becomes a sequence of countable reproduction cycles from the viewpoint of the next higher level. Within each cycle, the sequence of distinct phases will produce the impression of one-dimensional flow of time. Moreover, as long as we stick to a specific hierarchical structure (one of the possible sets of time scales), the direction from the lowest to the highest levels will establish yet another one-dimensional structure that effectively "pastes" the time flow of different levels into a universal time, like that we find in physics. However, time measurement is originally based on oscillatory motion; in physics, this requires a consistent treatment of any physical system on the same time scale, to make its states physically distinguishable. As the phases over several cycles become confusing, one needs either a statistical description, or a higher-level clock putting different cycles on the different sheets separating them from each other with specific singularities (branch cuts).

From philosophical viewpoint, the picture of hierarchical time, with a linear flow possible only within a higher-level period, is a consequence of the integrity of the world. Since the world is unique, and there are no other worlds (if they existed, we could rather consider them as the parts of the same unique world), any motion cannot be but an instance of the world's self-reproduction (though it may look like infinity for the creatures inside), and therefore all processes are repetitive, in the most general sense. On the highest level, any interaction means the world interacting with itself, and any change is a change within the whole, reproducing the same world in a different way. Since there is no higher level for the world as a whole, all instances of its reproduction are virtually indistinguishable, and the notion of time becomes inapplicable (as well as the notion of causality etc.).

With all those parenthetical remarks, let us return to the simple mechanical motion. In each frame of reference, the observer can label all the outer events by the instances of the inner time (not necessarily the same for different observers). If there is a spatially organized physical process, it can be used to establish a spatial grid, a local coordinate system. For instance, take a signal propagating with a speed c₀ in the frame of reference of each observer. We assume that space is homogeneous and isotropic, so that the speed of the dedicated signal is the same in any spatial point and in any direction; since we have nothing else to compare with, we cannot detect non-homogeneity and anisotropy anyway. Now, consider an infinite company of observers (the clones of the same observer) situated in different spatial points without moving relative to each other; this ensemble makes a frame of reference proper. Each observer informs the others about at any local event by sending a standard signal (presumably carrying some information about the kind of event). In this case, the distance from the current observer (the origin of the coordinate system) to any other is measured by the time (measured by the inner clock of the current observer) needed for the signal to come. For instance, the current observer can send out a signal and receive responses from all the observers on its way. The time delays 2Δt₀ thus obtained will form a spatial scale x₀ = c₀Δt₀. It is convenient to assume that these coordinates can be encoded in the signal (for instance, in the amplitude, frequency, or phase shift), so that any signal from a distant stationary observer carries information the unique spatial point. Similarly, one could suggest a synchronization procedure, so that the time variable would be the same all over the reference frame. In other words, the current observer (situated in the origin of the coordinate system) can receive information about any distant events marked by their spatial coordinates and a global time stamp.

Now, the current observer (in collaboration with the statically positioned colleagues) is ready to describe mechanical motion. Let some object move in the current reference frame, passing the current observer at local time t = 0; as it passes an observer located in a different spatial point, the current observer receives a signal informing about this event, with a delay Δt₀+Δt, which readily gives the velocity of the outer motion as

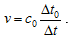
That is, we can only measure observable velocities relative to the reference speed c₀; there is no way to determine any absolute values unless we get yet another standard signal that could serve as an independent measure. Exactly the same holds for the observer moving at a constant speed v relative to the current observer: in his own frame of reference, the standard signal propagates with the same speed c₀, and all the other velocities can only be measured in the units of this standard speed.

This circumstance leads to a number of obvious corollaries. Thus, velocity measurement is only efficient at v < c₀; otherwise, the motion becomes apparently discontinuous approaching a stochastic mode, so that, instead of a moving particle, we observe a statistical distribution. This obviously means that the space and time scales bound to the reference speed c₀ are no longer enough to resolve the details of motion, and a shift to a different level is needed. This is a close analog of the well-known fact that, to resolve a spectral structure, we need a probe of a smaller wavelength (higher energy).

On the other hand, since velocities are measured in the units of the reference speed in all the frames of reference, the law of velocity addition is to be modified, to normalize the sum to the same fundamental constant c₀; in any case simple arithmetical addition of velocities will no longer be valid. Indeed, a reference frame is an inner space of the observer, and other observers can never get any information about its organization except through some outer communication. Since any velocity is measured in respect to a particular reference frame, it is an inner value that cannot be directly summed with similar values obtained in other reference frames. One needs first convert the inner value into an outer equivalent, and then convert it back to the inner value of another observer, to add to another inner velocity. In general, this is a nontrivial transformation, since the structure of the inner space does not need to exactly reproduce any outer structures. Although some correspondence (uniform for all observers) is required anyway, the methods of measurement may significantly influence the result. The usual relativistic law gives

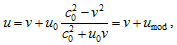
where u₀ is the velocity of a body for the observer moving relative to the current observer with the constant speed v. That is, to allow direct addition of velocities, we need to modify the value measured by the moving observer in a rather complicated manner.

This indirect interconnection of the frames of reference is immediately related to the constancy of the speed of light. Indeed, since we measure velocities relative to the velocity of the standard signal (for the present, this is the speed of light), the propagation of this reference signal will always be mapped into the reference frame as motion with unit velocity, regardless of the actual speed in the outer world. Even if the signal emitted by a moving observer carried information about the coordinates and time of emission, to allow any comparison, these values determined in the moving frame should first be converted to the frame of the current observer, which would effectively restore the unity of the reference speed, at expense of the modified notions of collocation and simultaneity.

Relativistic physics will certainly be valid and experimentally confirmed as long as we stick to "covariant" interactions essentially related to light. This absolute validity is ensured by the logical circularity involved in any interpretation. On the other hand, always remaining within the relativistic world, we do not even know where to look for any physical effects violating the symmetries imposed by the apparent constancy of the speed of light. One could believe that there is no way at all to detect such peculiar effects, and hence we are bound to eternally (within our local notion of eternity) stay covariant, leaving the other possibilities to some hypothetical creatures outside our observable Universe. Still, the philosophy of unism inspires hope, asserting the universal cognoscibility, the ability of reason to assimilate any aspect of the world. It is quite possible that physics beyond relativism is all around us, but we are not yet aware of the fact.