Time vs. Interval

The modern approach to special relativity is to merely postulate the symmetry group O(1,3) in the four-dimensional space-time, which assumes the invariance of the interval defines as

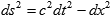
or, in the covariant notation,

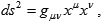
with x⁰ = ct and the standard signature for the metric tensor:

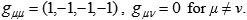
However efficient, this formal introduction can hardly satisfy anybody interested in the physics of space-time. Why should we choose a construction like this? Well, this choice agrees with the bulk of experimental data, and it works fine in the applications. Still, the nature of such unity of space and time still lacks clarity and we cannot indicate the physical conditions necessary for these equations to be valid, that is, the range of applicability for the special relativity theory. In physics, this should be considered as a serious drawback, an evidence of incompleteness, since no scientific theory can be universally applicable, and any closed theoretical system must clearly outline its scope.

The early explanations used to derive the invariance of the interval from a number of physical principles, such as the equivalence of all the space points and moments of time (hence translation invariance), the independence of the system's behavior of orientation (hence spatial rotation symmetry), and finally, the constancy of the speed of light in all the frames of reference (which leads to the symmetry in respect to hyperbolic rotations). Although one could contest the validity of argumentation, the very attempt to bind the foundations of theory to the common forms of human activity provides a basis for further investigation and the possible generalizations. Special relativity thus becomes a matter of experimental tests, rather than an abstract idea supported in an indirect manner by the validity of its implications, which is a very weak form of justification, since experimental setup is derived from the theory to prove, and therefore the results are expected to be compliant with it in advance.

There is yet another relativistic principle that does not follow from mere geometric symmetries, requiring certain assumptions about the character of dynamics. The famous Einstein's formula establishes equivalence of mass and energy: E = mc², with dynamic mass introduced as

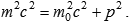
The nature of the rest mass m₀ is beyond theoretical discussion; however, everybody agrees that it should be dependent on the material of the particle and its inner motion. The rest masses of the so-called elementary particles are generally considered as physical constants, though some modern theories pretend to derive these masses from other, presumably more fundamental parameters.

The relativistic dynamics of a material point can be derived from the principle of minimal action if the action of a point particle is related to the interval by the equation

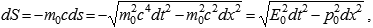
where E₀ designates the rest energy of the particle, while p₀ stays for a kind of momentum associated with the rest mass. Alternatively, one could consider the interval as scaled action; the role of variation principles in physics is yet unclear, though all the fundamental theories are traditionally required to comply with that formalism.

The idea of a kind of parity between space and time seems rather natural, since distances are practically measured by the time required to cover them in a standard pace. In particular, this could be the number of times necessary to apply a ruler to a segment of a line, or the time required for a light wave to propagate from one end to another. In relativistic physics, the logic is exactly the inverse: we measure time by the distance covered by light. This fundamental assumption seems to introduce a hidden logical circularity, and the independence of the speed of light of the reference frame may be an artefact due to the usage of light propagation as the measure of time. However, this circumstance does not play any important role as long as we have no other choice; postulating the constancy of the speed of light in the relativity theory, we simply forbid the very existence of such an independent measure.

Just to illustrate the possibility of an alternative treatment, let us rewrite the definition of the interval as follows:

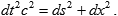
Comparing it with the definition of dynamic mass,

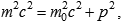
we observe a suspicious similarity, which probably is a mere coincidence, but which also may suggest a different interpretation of special relativity. Instead of reducing time to space, we could say that time results from the hierarchy of the particle's motion, including both spatial displacement and inner motion producing the rest mass. In this picture, the description of motion in the configuration space is dual to its representation in the momentum space, which is quite natural since the two space can be considered as mere Fourier transforms of each other. That is, moving along a virtual trajectory of the particle, we observe (or apply) a certain action, which, together with the length of displacement, determines a natural measure of time, and the variations of trajectories are to minimize this value. In particular, this implies the existence of the arrow of time: even for a particle at rest, time will always accumulate due to inner motion, and any explicit displacement will make it run faster. This is much closer to our intuitive notion of time, and the production of space-time by developing matter appears to be more straightforward and consistent. The invariance of the interval is then naturally explained by its correspondence to the rest mass as a constant of motion.

Although this approach may seem to violate translation invariance in time, this is not so, as long as the transition from one moment of time to another (the system's development) does not change the character of its dynamics (compare it with self-similarity in fractals). On the other hand, for some types of development (namely, those involving an inner reorganization or collective behavior), translation invariance in time will certainly get broken, and this perfectly agrees with our idea of irreversible dynamics.

In the hierarchy of motion, the cluster of spatial trajectories of one level becomes a part of the inner dynamics of another, and conversely, inner dynamics can always be unfolded in a kind of translation plus inner dynamics of a deeper level. In general, the levels of this hierarchy will have different natural measures of time associated with different reference processes. For instance, the inner time of a quantum system may result from an entirely new kind of interaction propagating much faster than light. This ensures an essentially collective behavior of quantum systems for a macroscopic observer, who will formally treat the virtual events as occurring "in no time"; hence the indistinguishability of particles and exchange effects.

The configuration space of inner motion is hidden from the observer; that is, it develops within a spatial point of the upper level. It looks like a particle can leave its "macroscopic" trajectory and get back without noticeable delay. In other words, inner motion can be modeled on the macroscopic level as virtual oscillations, so that their frequency would determine a part of the rest mass, along with a hierarchy of lower-level oscillations. In the plausible assumption that each level of hierarchy allows just a few modes of oscillation (standing waves), we come to a spectrum of masses, which will obviously depend on the level of consideration.

Now, the standard relativistic theory gets included in a general context, and the limits of its applicability can be discussed on a universal basis. We conclude that the constancy of the speed of light is equivalent to the assumption of the lowest (the most fundamental) level of matter; the versions of this assumption were put forth many times in the history of science, but they proved to be just temporary limits every time. Quite probably, a generalization of the theoretical scheme will get rid of many relativistic singularities, which are all due to the singular character of Lorentz group. The zero rest mass of photon means that we do not consider any inner motion; as soon as photons are allowed to undergo a series of virtual transformation, they will acquire non-zero self-energy; such "structured" photons will propagate slower. Physical vacuum is not an empty space, and therefore assuming any special role for the light speed in vacuum is nothing but a useful abstraction. Nothing prevents us from admitting a more complex organization of matter (including vacuum) and discovering new kinds of inner motion within photons. Who knows? Maybe a special role of gravity is to link one level of this hierarchy to another.