Among the Wise and Crazy

Philosophers have always irritated scientists with idiotic questions. Somehow, they are never satisfied with simple answers like "Oh, this is a trivial property of quasi-holomorphic convolutions of the bundles of Cayley algebras over the filters of residual catastrophes, in the Bayesian limit". No, they would ask again "But why do you think it should specifically be Cayley algebras?"—"Well, just because enveloped categories are octonion-valued. Everybody knows it".

Scientists are practical and solid; they have lots of things to discover, and even more things to predict. They have developed many useful tools that are very helpful in serious research since we do no longer need to unfold the whole from scratch, as the basic principles have long since been agreed upon, and it is the specific details of the observable behavior that are of real importance. The rapid development and the spectacular success of science are much due to this ability to accumulate experience in an exponential manner.

Philosophers are nothing like that. Instead of taking things for what they are and steadily extending the range of assimilated phenomena, they just want to know what that all means, and why it is that way. Instead of trusting the already acquired notions and proceeding to more complex cases, they turn to the primitives every time they need to consider a quite familiar problem, with reinventing the whole philosophy as if it had never existed before. Instead of plain and unambiguous decisions, they stay oblique and elusive. That is, instead of producing answers they produce questions. And then, serious people have, instead of discussing the important issues of anthropic landscapes on a 13-brane, to resort to a sort of queer gesticulation in order to bring the overall impression of something to those who don't understand the sheerest basics of supergravity and cannot tell cis-variation from trans-mutation.

Every course of theoretical physics starts with a brief exposition of the variation principles used to derive the equations of motion and other dynamic features. This is a well-established approach that has proved to be universally applicable and productive; physicists have employed it for a few centuries. For an ignorant philosopher, the usage of variation principles in physics will always remain an unintelligible mystery, a technical trick beyond any reasonable comprehension. They ask why is it that we should believe in the stationarity of the action in respect to the possible infinitesimal variations. The primitive quasi-animistic explanations of the founders of the classical mechanics are not enough to convince a modern person (unless this is a physicist). Mere postulating the fundamental principles is hardly tolerable even in mathematics, and that is why mathematicians have never stopped probing the foundations of their science. So, why? Is there any physical sense in the variation procedure, to make it scientific method rather than scientific prejudice? And what if we do not stick to stationary manifolds but rather consider dynamically shaped motion? Is there a kind of higher-level dynamics to regulate the transitions from one stationary world to another?

The general question about the applicability of variation principles would specifically touch upon the scope of variation. Traditionally, physical motion is treated as spatial motion (in a many-dimensional configuration space), and we vary the positions, velocities or accelerations of the moving points. However, a physical system is also characterized by a number of physical parameters that do not enter in the general variation scheme, though their variation could essentially change the character of motion. For example, the mass of a material point is used to keep intact in the traditional variation principles, nothing to say about fundamental interaction constants (which then appear to be not so fundamental, in view of the possible renormalizations). However, nature is not obliged to keep the structure of the Universe stable for our convenience. All the physical characteristics could vary in real motion, and hence be subject to variation in a theoretical model. As an act of absolute arrogance, we could even assume the possibility of varying the fundamental mathematical constants like π and e. Why not? Mathematics is an abstract reflection of a certain manner of our doing things in the real world; quite probably, in some yet unknown sphere of reality, essentially different ways would be needed, and the very notion of mathematics would change.

Finally, any variation principle at all (either differential or integral) is essentially nonlocal. The very possibility of comparing simultaneously taken trajectories (however infinitesimal) assumes their presence as a whole within the same reference frame. One can only wonder how it happens that we can derive local physical theories from such nonlocal considerations. This objection is probably not so serious for classical mechanics (which does not restrict the notion of simultaneity) and quantum theories (as they are nonlocal by their nature, taking the whole configuration space as a given construct at any instant); however, in a relativistic approach, the possibility of comparing the points of space-time separated by a space-like interval provokes doubts in the overall consistency. A similar (though possibly not as thorny) issue is related to the possibility of relativistic thermodynamics. Any statistical theory is based on the (at least principal) comparability of the parts of the system within the whole, regardless of their spatial or temporal separation. A consistent relativistic statistics is therefore to be restricted to small systems with inner changes being much slower than the relaxation speed; otherwise, any local motion would destroy the integrity of the system and break the statistical regularities. But this requirement is obviously equivalent to considering slow, non-relativistic movements. Somehow, we need to combine the two levels of consideration, with relativistic motion "embedded" in a classical frame, or conversely, a classical system moving fast as a whole.

A whole bunch of silly questions is about the frames of reference and relativity. For instance, what is the nature of a reference frame? Does it correspond to anything real in the physical world? Or, is it rather an artificial construction, just to describe the way we treat the world in our practical activity? In other words, does it refer to a physical system or to an observer? This problem is closely related to the question about the structure of the reference frame. Thus, in the latter case, all the systems can be placed in a single frame and therefore always remain comparable; on the contrary, there is no reason to admit the similarity of reference frames associated with different physical systems, albeit of the same kind. One could also think of some intermediate possibilities.

For instance, do we need to assume the orthogonality of the spatial axes in all the frames? If the frames were the inner constructions of the observer used to map the observable events, universal orthogonality would be a reasonable choice, characterizing the type of observer regardless of the objective (physical) behavior. However, in this case, the meaning of the relative motion of different observers is an open question, as the individual reference frames cannot be directly compared, hidden inside the observers (the frames themselves are not observable). On the contrary, if the axes of a coordinate frame are physically constructed (by the observer or any other physical system), they must be subject to changes due to the relative motion of the reference frames. Thus, let observer (frame) S' move in respect to observer S along the X-axis common for the both observers (save for the variable displacement of the origin), with the speed V; now, let observer S' construct the Z'-axis as the trajectory of a standard signal (a probe) propagating with some speed c' perpendicularly to the X'-axis. For the stationary observer S, the propagation of the probing signal (possibly with a different velocity c) will no longer be orthogonal to the X-axis, as shown in the picture:

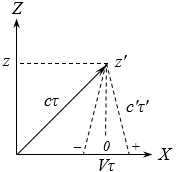
When the probe arrives to some point z (in τ seconds, or billion years), the position of the moving observer on the X-axis of S will depend on the balance between the speeds c and V. In the traditional relativism, the origin of the frame S' in relation to the frame S will come to the point 0 right below the destination point, so that the observed axis Z' will remain perpendicular to axis X'. But it may also lag behind, as in the (–) point, or run ahead, as in the (+) point; in such situations, a moving reference frame will no longer be orthogonal for the stationary observer.

Of course, such void speculations have nothing to do with physics, since the validity of the relativistic picture has been confirmed in tons of experiments, and there is just nothing to discuss. But a philosopher will always ask why.

Yet another philosophical idiotism questions the meaning of the well-known Lorentz transform. The independence of the speed of light of the motion of the source is an experimentally established fact; so, what is the problem? However, considering the correspondence between the coordinate systems in a moving frame and a frame at rest, a philosopher finds it strange that the law derived from the constancy of the speed of light happens to be singular, effectively dividing the whole space-time into mutually isolated regions. How this could happen, if we considered the coordinate systems defined on the whole space-time within each frame, without any exemptions? And how, within a particular frame of reference, we could introduce coordinates in the regions that are physically inaccessible? The situation cannot be improved with the admission of strictly local coordinates, since we still need to attach a whole Minkowski space-time at each point of the physical manifold, but such a global structure, even treated as an inner space of the point, is incompatible with relativistic covariance. In view of that all, the very assumption of the three spatial dimensions is already highly problematic.

To add confusion, a philosopher would object that the constancy of such an obviously non-covariant characteristic as three-dimensional velocity should be laid in the basis of a covariant (relativistic) theory. One could expect that the fundamental quantities of a theory should be defined in a manner consistent with the structure of the theory. That is, a value that is not generally preserved in the transition from one reference frame to another can hardly be physical enough to pretend to the rank of a fundamental constant. Though we can always tweak the velocity addition law to preserve this particular value, it looks much like an ad hoc solution, and one would keep wondering, if there were other, more consistent possibilities.

From the logical (philosophical) viewpoint, the singularity of the Lorentz transform does not imply the impossibility of faster-than-light motion. Well, we cannot (so far) get through the light barrier; but what if somebody (or something) is already moving faster than light in respect to earthly observers? In the own frame of reference, this object will be at rest, and nothing prevents it from living a full-scale physical life. Though humans do not exist for such a hypothetical observer (as faster-than-light objects), there are many other objects that move with under-light velocities in this reference frame, and a variety of observers reproducing the structure of the observable world of a human. The whole world thus becomes a cell structure, with each cell isolated from the others by the light barrier, but otherwise a quite traditional physical reality, as far as its inner motion is concerned. Since the principal question of philosophy is about the integrity of the world, the unity of the cell Universe must logically be established through a different kind of interaction (essentially nonlocal from the relativistic viewpoint) that would allow some physical manifestations of the isolated worlds within each other. Quantum physics suggests exchange effects for an obvious candidate. Thus, if all electrons are physically equivalent and one can always be replaced with another, the electrons of the separated worlds could enter the same antisymmetric collective state, and exchange effects would link one world cell to another. In this picture, light barrier is just like any other quantum barrier, and it could be penetrated by ordinary particles, with some probability. Nothing prevents us from picturing any other channels of cross-barrier interaction.

The nature of space and time has fascinated philosophers for centuries, and they invented all kinds of metaphysics to derive the well-known facts from sheer abstractions. Thus, the dimensionality of space was among the favorite "hard" questions, until physicists, to stop further speculations, just said that there is no any fixed dimensionality at all, and the number of spatial dimensions can be arbitrarily chosen to satisfy the needs of yet another theory of everything. We live in a 3D version of the Universe, and this is nothing but a coincidence, a broken symmetry; it is legal to ask how it should be broken to allow the existence of the humanity, but there is no reason why. It simply is that way, and we have to merely accept it as an actualized possibility.

Still, the geometrical topic is almost inexhaustible, and those who like to roam their doubts will always find a sticking point. For instance, one could attack the very analytical method, and get deeply astonished by the standard vector structure of space. Indeed, why do we chose a quadratic form for the distance? In mathematics, there are other kinds of metric, and the adherence of physics to one particular form is at least strange. By the way, in economy, we can simply sum up the costs of quite different origin, and there is no need for vector addition. The traditional structure of the physical space seems to hold only in the vicinity of some equilibrium point, with the usual coordinates referring to the departure from the balance (with the linear terms cancelling out).

The very notion of a spatial point is already a cause of trouble. In physics, all the meaningful concepts are finite; the physical world does not know any infinities or infinitesimals. This means that phenomena of very different scale cannot be treated within the same physical theory. In particular, a spatial point of one level may correspond to a whole space on another. In principle, this relation can be mutual, so that a lower-level point is also a contracted form of the upper-level space. For a common example, recall the duality of canonic variables in classical and quantum mechanics. Each point of a manifold is equipped with a tangent space, while each point of the tangent space is a class of trajectories in the base. The philosophical part begins when the possible depth of such hierarchies is in question. Metaphorically exploiting the existence of compound systems that behave as a whole in respect to some outer interaction, one gets interested whether the spatial points could be treated as such collective effect rather than a fundamental primitive. Of course, the same problem with the instances of time.

However, time is a much more mysterious entity. Its dimensionality, relation to space and the lack of isotropy (referred to as the arrow of time) is a permanent attraction for void curiosity. Stubbornly opposing the relativistic union of space and time, philosophers would anyway ask why such unification could be possible. Presumably, an explanation would indicate the limits of this picture, the practical situations where the qualitative difference of space and time would be essentially irremovable. In a way, thermodynamics and nonlinear dynamics suggest the notion of irreversible and non-uniform time. However, such overall behavior is still a superstructure of the usual physical interactions that are symmetric in time. But what if the asymmetry lied already in the vary grounds of all?

In our everyday life, time is always associated with some repetitive activity. The higher is the repetition rate, the faster runs the corresponding inner clock. Entirely in correspondence with relativistic physics, more effort is needed to speed up the things; time is thus subjectively related to energy. The hierarchy of inner time closely resembles the hierarchy of time scales in physics. Here comes an ignorant philosopher with the same silly questions. Why do we think that physical time can be associated with a single number, all physical existence labeled by the positions on the same time axis? Why not admit that time is essentially relative, different time scales not necessarily being comparable? This would be quite analogous to the cell Universe implied by the singular Lorentz transform, with the same interconnection issues.

In any case, the very treatment of time along with the spatial coordinates is not at all a decided thing for a philosopher. Despite all resemblance, there is a significant difference, whether we talk about the state of a physical system (its configuration), or its motion (a sequence of states). One can certainly introduce the notion of the state of motion; but that would be a different level of hierarchy, and its projection into the lower-level configuration space is only possible in some special physical conditions. Even allowing for such possibility, we still cannot directly map time to the configuration level, though this could be achieved associating time with a particular kind of motion and then comparing the state of that reference process with the accompanying changes in the system's configuration.

Holding that in mind, one would wonder whether it would not be more reasonable to first sort out the inter-level projections, before trying to pack time in there. To be specific, take the two adjacent levels: spatial positions and momenta of material points. Traditionally, the current state of the system is determined by the collection of positions and velocities (which virtually allows us to guess for the next set of positions, while a prediction of new velocity values additionally requires the knowledge of accelerations, and so on). From the dynamic viewpoint, momenta are preferable over velocities in the characterization of the system state (which, by the way, raises the question about the static mass momenta as primary to mere spatial positions). The difference of the adjacent in time system states is then characterized by the collection of spatial displacements and the infinitesimal change of momenta (a displacement in the phase space of the system). Time itself is out of the scheme, as it refers to the overall scale of the system's motion, the level of detail we take into account. Including time in the construction of any invariants (like in the structure of the relativistic interval) is therefore equivalent to the explicit specification of the scale, that is, the assumption that the system cannot evolve in its motion to get from one level to another, or rearrange the entire sequence of levels. In a more general approach, we would rather consider the trajectories in the phase space and seek for symmetries in this extended space; this would provide a natural basis for considering dynamically broken symmetries (as we do, indeed, in nonlinear dynamics). In this picture, the scale of time would the derived from the state of motion rather than rigidly built into the theory. For example, the presumably invariant interval could be constructed from both spatial coordinates and momenta, as something like

.

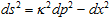Now, let dp and dx contain two components of very different scale: a smooth (almost inertial) trajectory on the higher level and very fast circular motion on the lower level, with the radius much smaller than the "macroscopic" displacements. In this case, we approximately obtain

,

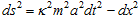which readily suggests the idea of a reference speed resulting from some hidden periodic process; obviously, the validity of thus obtained "relativism" is restricted to the domain of stability of that inner motion. Moreover, the presence of a number of oscillation with very different frequencies will naturally introduce a hierarchy of time scales.

All right, let us move on to spoil the feast of general relativity as well (or as malignantly). The fundamental principle of the equivalence of gravitational and inertial mass leads to the formal equivalence of gravity to inertial forces, that is, the apparent forces that act on a mass whose motion is described using a non-inertial frame of reference. The idea seems physically attractive, since there physical motion can never be free in an absolute manner (otherwise, we could never learn about it), and one can never tell an inertial frame from non-inertial. In classical mechanics, inertial forces are considered as fictitious, while general relativity treats them as real physical forces akin to gravity (which allows, for instance, considering the emission of gravitons by a rotating body; sooner or later, we're going to catch such gravitational waves, just because we want it so much).

But now, a stinky philosopher comes in and (with a wry smile) congratulates us on becoming true dialecticians in establishing the fact that the motion under the action of an outer force is indeed free motion! A good piece of work, isn't it? On the other hand, general relativism means that there is no longer any distinction between an experimental result and an artefact; all results equally go. In a higher dialectical sense, this is quite an achievement, an appreciation of the fact that any observation depends on both the thing observed and the observer. That is, human actions develop in the real world, and whatever we do is bound to reflect some objective features possibly worth studying. A blunt error of an experimentalist, who, for instance, has incidentally swapped the polarity of power supply, could lead to miraculous discoveries; a mathematical error in processing the results could be a sign of some intricate interdependence between the physical phenomena and human psychology, while any effects of the finite digit capacity in a numerical simulation would indicate indeed a universal physical regularity.

Then the same philosopher would spitefully ask how the physical reality of non-inertial reference frames is to comply with special relativity. It may seem that, for instance, a rotating observer has to admit asymptotically infinite velocities (and an infinite inertial force to keep the world turning). One does not need any astronomic distances: for an observer, sitting on the hard disk of a computer in New York, the whole Europe is already in the far tachyon region. When I turn on my computer somewhere in Moscow, all the Americans are to experience a huge gravitational shock, and I just don't know why they have not yet been entirely exterminated (in God we trust!).

Of course, the philosopher will never swallow the standard answer that any reference frame is defined in a local manner, and it cannot be extrapolated to infinity. This explanation does not clarify the issue, since it the criteria of locality remain vague and arguable; moreover, the existence of any cut-off value for the spatial distance is an additional (and rather strong) physical assumption (virtually equivalent to the discreteness of space-time). Yet another standard explanation that there is no such thing as an absolutely rigid body and the outer regions of the Universe will rotate slower than those in the vicinity of the observer is also rejected with disgust. Indeed, the rotation of the observer is their personal problem, and the rest of the Universe won't much care for it, unless the observer is heavy enough to produce a significant effect on the structure of the whole Universe. But this effect is never taken into account when we simply switch from static Cartesian to a rotating coordinate system, practically in no time (as the very possibility of transform is based on considering the two coordinate systems in parallel). When a ballerina performs the standard 32 fouettés, she immediately sees the whole world to spin around her, though the light from the Sun has to travel to the Earth much longer than the whole performance. How this apparent motion is related to real forces is still an open question. A philosopher could only accept the equivalence of gravity and acceleration as a manner of expression, a witticism, a play of words, rather than a physical principle. Yes, the forces in an accelerated system can add up as if there were some additional source of gravity. It does not mean that the nature of the additional force is the same as the nature of gravity; it only indicates that, in an accelerated frame of reference, one cannot directly measure gravitational effects, requiring certain formal manipulations to account for the observer's acceleration. This is exactly the same procedure we use in astronomy to derive the physical movements of the celestial bodies from their apparent motion relative to a local observer placed at some geographical point and measuring time with a locally calibrated chronometer. Similarly, we cannot use a barometer to measure the altitude unless we know the current atmospheric pressure at a reference level; and even then, to separate the value of interest from the incidental influences, we need to account for the profile of humidity and the distribution of wind velocities, along with any other observation conditions.

In the popular (and even philosophic) literature, there is much enthusiasm about the equivalence of mass and energy, presumably discovered by Einstein. In fact, Einstein has never really established anything like that; he only found that the relativistic motion of massive bodies requires accounting for the velocity of the body in a way that looks like the increase of mass for higher velocities. This apparent behavior says nothing about the nature of body's mass as such (the rest mass). The only logical conclusion one can draw from relativistic mechanics is that that a physical observation can never produce any direct evaluation of a body's mass, requiring additional procedures to extract the quantity of interest from experimental data. But, again, this is a common characteristic of any measurement at all, and one does not need to be a physicist to become aware of that circumstance. For instance, the common electronic bathroom scales (at least the economic-class models) will display a significantly higher value if loaded abruptly, with a jerk; that is why one needs to apply the weight gradually, avoiding any additional push. Using the "relativistic" logic, one could interpret it as the equivalence of mass and momentum…

Following the same line of reasoning, a philosopher would risk to raise a huge wave of indignation and contempt declaring that, in special relativity, the Lorentz transform does not imply any real equivalence of space and time; it only means that the observable space and time do not coincide with the formal coordinates used in relativistic mechanics and hence these latter cannot be (at least) directly measured. The statement does not seem too strong, compared to the entirely traditional convention that spatial coordinates and time in quantum field theory are not observable at all.

Silly remarks of that type can proliferate to infinity. Experimental procedures are extremely vulnerable in this respect, as they depend on numerous factors difficult to track. On these grounds, some theoreticians declare that physical theory does not depend on experimenting at all, and no experiment can influence its inner truth. Some philosophers object that a physical theory is meaningless without any practical implications; on the same footing, they spoil the reputation of experimental science questioning its objectivity and precision. Thus, the traditional statistical methods leave a philosopher bewildered and perplexed. Why do you think that averaging should increase the accuracy and objectivity of observation? Even if it does in many practical cases, this is not the reason to believe in its universal power. Any statistics is based on a number of assumptions; the random nature of fluctuations is possibly among the strongest. Even accepting the probabilistic picture, one still needs to guess the type of statistical distribution, which may essentially depend on the range of phenomena to study. Everybody knows that experimental results may contain systematic errors (with their own distribution of fluctuations). In most cases, such influences cannot be eliminated or reduced. Experimentalists usually do their best to detect the source of error and purify the results applying all kinds of mathematical processing; however, this makes the result essentially indirect and less trustable in the context of theory validation. There is always a suspicion that the intricate methods of "normalization" applied to experimental data serve, in fact, to impose an a priori theoretical model, so that, instead of studying nature, we adapt it to our conceptual preferences. Such an approach is all right in engineering, as long as we can keep control over the critical parameters. In science, it may seem too biased and possibly misleading.

In any case, there are different directions of research. Mostly, we are interested in general laws that hold on the average. However, one can also be interested in the individual manifestations of these laws in the infinite diversity of real situations. A deviation from a mass regularity is as objective as the regularity itself, and a closer look may bring insights into entirely new aspects of the application area. For example, a general theory of literature may be interested in the typical forms and the common trends; on the contrary, in the work of an individual writer, the characterization of the individual style is often much more important that the traces of all kinds of tradition and the influences of a certain literary school. Once again, we come to a hierarchical picture, with a qualitatively different science on each level.

Luckily, scientists rarely listen to philosophers; and they are certainly right. As one of my physics teachers used to say, all the questions "why?" are sheer demagogy. If you ask a scientist, why it comes to this or that particular choice, the answers would largely vary:

— Because everybody does it that way.
— Because it's cool, and I like it.
— Why not? Just to see what happens.
— Because I need to feed something to the peers to get published.
— Because I want to sell it to the DOE for a grant.
. . .

The right answer is "I don't care". It is not up to a scientist, to ponder upon the reasons of scientific research. Let scientists do science—and philosophers do the rest.