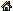IntroductionIt is a well-established fact that psychological processes are hierarchically organized [1]. Today, all artificial intelligence constructions are hierarchical in one way or another. Since the end of the 1960s, the tendency toward a multilevel description of art phenomena, as well as of the processes of artistic creation, has been gaining strength [2]. But the time has come to move from the abstract opposition of different levels in empirical classifications to the investigation of the mechanisms of the formation of those levels, up to the development of closed mathematical models. L.Avdeev and I have recently built one such model; it describes the formation of hierarchies of musical scales on the basis of the informational comparison of sound complexes [3]. This model will illustrate the general statements of this article. Sensation and PerceptionIt has been noted, ever since the science of psychology took its very first steps, that the interaction between a person and the world involves the levels of sensation and perception, with both differences and interrelations between them. Sensation is the process of active structurization of the object situation facing the subject [4]. This structurization proceeds on the basis of the subject's conceptions (individual patterns for describing situations) and sets (which delimit classes of conceptions). Sensations "encode" the stream of physical and psychological stimuli, combining symbols from a given collection. Perception, in its turn, deals not with signals that are external to the subject but with subjective representations formed in the sensory process. This is the level where logical operations take place, relating a situation to a definite class and estimating the satisfactoriness of its description within the present set. If the set is not adequate, a new collection of conceptions is formed, one that is better suited for the current activity. This formation of new conceptions is a kind of prognostication of the development of a situation which corresponds to the notion of conception as a process. The new set influences both sensation and perception, and thus the entire process circles back to the same point in an upward-developing spiral (Fig.1).
For a theory of aesthetic perception, it is important to distinguish between the emotional reactions accompanying sensation and perception. On the level of sensation, emotions are controlled immediately by incoming signals. The even sound of a pure fifth, the definiteness of a clear color, the smoothness of a line or the simplicity of a texture are felt in this way. The level of perception elicits emotions of appraisal, of the "like/do not like" type. Here it is not the situations themselves that are emotionally felt, but their organization and conformity with the subject's sets. Thus a work of art can excite similar sensory emotions in different persons, while perceptual (subjective) emotional reactions can differ rather significantly. Here, in fact, one can speak of aesthetic feeling proper [5]. On the face of it, subjective feelings are too diverse to systematize. Nevertheless, my hierarchical approach implies the possibility of discovering a "common core" in the variety of conceptions, that is, the conceptions induced by the logic of the phenomenon itself and human psychology, rather than an individual's history. DiscordanceThe appraisal of a situation in the "like/do not like" manner can be described by the concept of discordance. For elementary perceptions, which are mathematically represented by (multidimensional) Gaussian distributions [6], discordance can be evaluated as the quantity of information introduced into a situation by one stimulus appearing on the background of another (Fig.2) [7]. Thus a feeling of discordance arises in the chain: first stimulus — selection of conception — second stimulus — shift of conception — discordance.
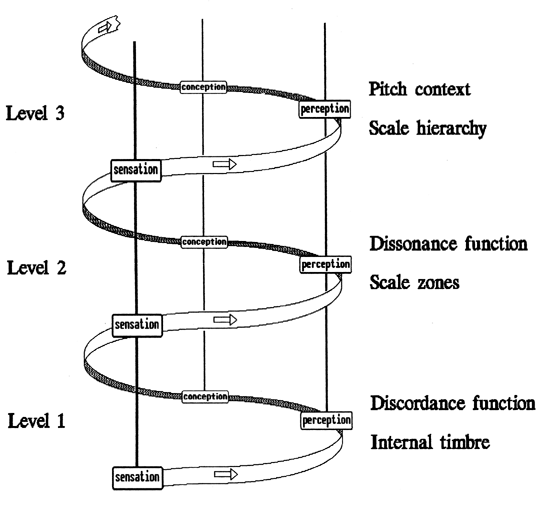
The relation of discordance is symmetrical, that is, it does not depend on which of the stimuli comes first in the chain. More complex conceptions can be represented by combinations of elementary conceptions. In music, this is the natural distinction between the principal tone and the overtones. There are analogous elementary conceptions for other arts as well. Thus, in painting, it is possible to define a "generalized point" of finite dimensions. In traditional poetry, this role is played by the elements of articulation. For this theory to work it is essential only that elementary conceptions form a manifold that is topologically equivalent to Euclidean space. Modern data on physiology of analysers and psychophysics of perception do not contradict such an assumption [8]. However, much of what is important for the practical investigation of the mechanisms of the transformation of a physical signal into a collection of elementary conceptions is still in the initial stages of development. The difficulties are not so much experimental as conceptual: we lack concepts to describe the internal, subjective image of an object situation. The hierarchical approach overcomes this deficiency, to some extent. As soon as I define the concept (and the value) of the discordance that characterizes the subjective compatibility of two elementary conceptions, the discordance for compound conceptions can be readily evaluated. Complex conceptions are collections of elementary components, each of which is supplied with an "amplitude" [9]. I find such a description quite analogous to the quantum-mechanical decomposition of a state vector in some basis in a Hilbert space. As in quantum mechanics, the amplitudes are normalized, so that the sum of their squares equals 1. I also use the "overlap integrals" to compare complex conceptions, that is, the sum of the component products of the amplitudes for two vectors — again, following the methods of quantum mechanics. Thus, to evaluate the discordance for compound conceptions, I evaluate the discordance for each pair of elementary components and then sum up the results multiplied by the respective amplitudes. In the discussion that follows I will refer to the components of a compound conception as harmonics and to the collections of amplitudes as subjective or internal timbres, by analogy with the perception of music. In music, where the frequencies of harmonics are strictly bound to the frequency of the principal tone, discordance for two compound sounds depends only on the distance (the difference of pitch) between their principal tones. Figure 3 shows that this function has a number of distinct minima [10]. This means that sounds with a corresponding difference in pitch are the least at variance with each other and can belong to the same tone system. This collection of sounds forms a scale that any other sound is then compared to; a coordinate frame in which musical thought spreads.
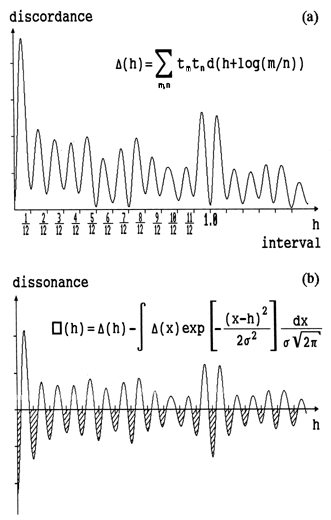
DissonanceThus the informational comparison of conceptions leads to the formation of perceptual scales. Perception appears to be highly organized and reveals an internal regularity. But how does a specific sound relate to a scale? It has been established experimentally that it is the nature of any scale to consist of zones, which means that many sounds may belong to the same degree of a scale, if they do not differ very much [11]. In particular, all the sounds close to a minimum of the discordance function should form a single zone. Then it is natural to attempt to filter out the "variable constituent" from the discordance function by subtracting a locally defined "average level". As a result, the dissonance function is obtained, the sign of which indicates the correspondence of a stimulus to a scale set (Fig.3). The areas of negative values of the function form the scale zones. Any sound within a zone represents the same degree of the scale. Sounds with positive dissonance values can be called dissonances proper. The relativity of dissonance is an important corollary [12]. It is not the combination of sounds by itself that produces the impression of dissonance, but rather the sound's overstepping the limits of a fixed zone structure. That is why sound combinations that are dissonant in one scale might not be dissonant in another. Of course, this applies to the other arts as well. Scale HierarchyThe collection of scale zones is not the only information the subject extracts from the discordance function. As a matter of fact, this construction picks out its principal rhythm. But in addition to this principal rhythm, there are other rhythms in the discordance function that define the substructures possible in the scale. They all can be detected by the maxima of the Fourier transform of the discordance function, and for every such substructure, the dissonance function is calculated in the usual way, that is, the scale zones are defined. The collection of zone structures "embedded" in one another forms the hierarchy of scales, the highest level of the scale set. Scale hierarchy plays a significant role in painting as well. In poetry there is an analogous hierarchy of rhythmic formations. Since the results I obtain within the hierarchical approach are quite general, I conclude that any kind of aesthetic perception implies a movement from large fragments to ever more minute details. The elaborateness of the scale hierarchy characterizes both the intensity of perception and the profundity of the work of art itself. Mathematically, rhythms in the discordance function are represented by the corresponding frequencies (for example, the number of scale degrees in an octave). The frequencies, in their turn, are directly related to the "fuzziness" of elementary conceptions (the dispersion of the Gaussoids), as well as to the number of perceptible components of a compound image. Thus the transition from the principal scale to the possible substructures corresponds to a "coarsening" or "relaxing" of perception. Perception filters out the details of an integral image, which fit into a scale set. D.Marr illustrates this process in the case of visual perception [13]. But there is a novel point in the hierarchical approach: not just any perceptual tuning is possible, but only a few of discrete levels! Optimal ScalesThe above discussion does not imply any restrictions imposed on the structure of multicomponent conceptions (internal timbres). Physically, signals of arbitrary structure are possible. However, sensation does not simply transmit these signals to the subject but also separates the two sides of a signal: its coloring (tints and variations) and its quality (the relatedness to a definite class) [14]. It is commonly known that the coloring of sound does not, as a rule, hinder the perception of melody and harmony in music. The same composition can be performed with different kinds of instruments and it would be recognized and perceived in much the same way. Other examples of this are the perceived similarity between a painting and its black-and-white reproduction, or a printed poem and its oral recitation. Naturally, there are differences. But a common base is also felt, which implies the presence of a number of invariants [15]. One such invariant is the scale hierarchy, which is completely determined by the internal timbre [16]. Therefore, each timbre describes a class of scales as an invariant of musical performance. The logic of the hierarchical approach leads one to expect that not just any timbre, but only a finite number of fully determined subjective timbres would exist. One can ascertain exactly which timbres are distinguished by perception using two criteria: robustness and regularity. Robustness (a number between 0 and 1) gives the measure of a timbre's preservation (in the sense of maximum overlap, as discussed in the above section entitled Discordance) under various nonlinear transformations, which it inevitably undergoes in psychophysical processes. For a finite number of components, the upper limit of robustness cannot be reached. Timbres with a robustness greater than 0.5-0.6 can be considered quite stable. Regularity describes the markedness of rhythms in the discordance function and, first and foremost, of the principal rhythm. In other words, the zones of the principal scale must be well separated in perception. This requirement is expressed mathematically as the maximization of the value of the Fourier transform of the discordance function in some point. The possible positions of the maxima give the possible regular scales. I say a timbre is optimal if it is both robust and regular. Optimal timbres set the possible scale hierarchies in perception, the standard classes of perceptible situations. It turns out that, in pitch perception, both robustness and regularity can be reached simultaneously only at the points that correspond approximately to an integer number of scale degrees per octave. Some of the optimal timbres obtained by L.Avdeev [17] are shown in Fig.4. Notice that the number of harmonics in the optimal timbres increases with the lessening of the dispersion (the sharpening of hearing). However, the higher harmonics, as a rule, merge into one chromatic formant determining the articulateness and coloristic resources of the scale. The lower harmonics also group themselves into formants [18]. The principal part in the description of the artistic potential of a scale is played by the harmonic formant (from the principal tone to the first "hole", or a harmonic with 0 amplitude) and the modal formant (the second or, sometimes, the third group of harmonics). The size of the harmonic formant determines the intervals that can be used in harmony. The modal formant characterizes the features of melodic movement. The ratio of the formants provides an additional value that is important for the description of scales: lability. I have noticed that melodics dominates when lability is positive and harmony dominates at negative labilities. Lability less than -1 points to the suppression of melodics and the indifference of harmonic functions (harmonically labile scales). Lability greater than 1 testifies to the decentralization of melody and the infirmity of modal functions (modally labile scales) [19]. If the absolute value of lability is less than 1, the scale can be called stable. Such scales prove to be the most universal in their applications.
On the basis of the calculations made, one could investigate the peculiarities of the usage of various scales. Thus I suggest a new language in the theory of music to describe pitch phenomena in a more adequate way. General ConclusionsThe perception of a work of art reveals its intrinsic hierarchy of scales. This hierarchy is specific to each particular work; and yet it is not arbitrary, but an element of a discrete collection. A good work conveys the scale hierarchy conceived by its author to any sufficiently practiced observer. However, the artist's intentions cannot always be satisfied with the available material. For example, the performance of dodecaphonic music in the 12-tone tempered scale does not reveal the internal connections specific to each series [20]. On the contrary, the 12-zone "hypermodes" naturally appear in the scale hierarchy of the 19-tone scale (Fig.5). The presence of a theory quantitatively describing the scale hierarchies makes the search for a means of expression more purpose-oriented.
I have described how the theory of hierarchical scaling in aesthetic perception aids the understanding of some important features of pitch relations in music. The mathematical model makes use of a simple one-dimensional representation of an elementary conception, and takes into account the achievements of musical theory, as well as detailed physiological and psychophysical data. Other arts have not been so fully investigated, and their quantitative description is yet to come. In music itself, it still remains to generalize the results of this model to the multidimensional case, allowing for the rhythmic and dynamic aspects, in addition to pitch. The hierarchical theory of aesthetic perception has a long and strenuous life ahead of it. References and Notes1. K.H.Pribram, Languages of the Brain (Englewood Cliffs, NJ: Prentice-Hall, 1971); Perception: Mechanisms and Models (San Francisco, CA: W.H.Freeman, 1972); R.M.Granovskaya, Perceplion and Memory Models (in Russian) (Leningrad: Nauka, 1974). 2. A.A.Moles, Sociodynamique de la culture (La Haye: Mouton Paris, 1967); E.Regener, "Layered Music-Theoretic Systems," Persp. of New Music 6, No.1, pp. 52-62 (1967); E.V.Nazaykinsky, Logic of Musical Composition (in Russian) (Moscow: Muzyka, 1982). 3. L.V.Avdeev and P.B.Ivanov, A Mathematical Model of Scale Perception (in Russian) (Preprint P5-90-4 of the Joint Institute for Nuclear Research) (Dubna, 1990). 4. The interpretation of sensation and perception that I present in this article has not won general recognition and is a characteristic feature of my theory. 5. This is a key point of my theory. Most mathematical researchers, including Pythagoras and Helmholtz, have tried to describe aesthetic feelings exclusively on the basis of sensory processes, which always led to contradictions and strained interpretations. The connection of the subjective factor makes the theory much more logical and nearer to intuitive understanding, and also brings it into correspondence with contemporary experimental data. 6. H.L.F.Helmholtz, On the Sensation of Tones as a Physiological Basis for the Theory of Music (New York: Dover, 1954). 7. See Avdeev and Ivanov [3]; and G.A.Golitsyn, "Information and the Laws of Aesthetic Perception" (in Russian) Number and Thought, No.3 (Moscow: Znaniye, 1980). 8. S.A.Gelfand, Hearing: An Introduction to Psychological and Physiological Acoustics (New York: Marcel Dekker, 1981); Elements of the Theory ol Biological Analysers (in Russian) (Moscow: Nauka, 1978).
9. Avdeev and Ivanov [3].
10. Curves such as the one in Fig.3a
were already being obtained experimentally by Helmholtz
in the nineteenth century but they have never received
further interpretation.
11. N.A.Garbuzov, The Zone Nature of Pitch Hearing
(in Russian) (Moscow, Leningrad: USSR Acad. Sci., 1948).
12. Most theories of aesthetic perception cannot explain
this quite common phenomenon in the arts.
13. D.Marr, Vision: A Computational Investigation
into the Human Representation and Processing of
Visual Information (New York: W.H.Freeman, 1982).
14. Quality, from the point of view of the hierarchical
approach, is something that cannot be removed from an
object or modified without making it something else.
Naturally, the distinction between "coloring"
and "quality" depends on the level of scrutiny.
It is easy to find instances of mutual transitions between
the two categories, illustrating the mutual reflection of
ideas in general (in the sense of Hegel's dialectics).
15. R.K.Zaripov, Computer Search for Variants in
Modeling the Creative Process (in Russian) (Moscow:
Nauka, 1983).
16. There are a number of concepts in psychology that
are widely used in connection with the subjective
representation of situations: mental structures, functional
systems, gestalt, etc. Tracing the relations between these
concepts and scale hierarchies would produce another article
more fit for a psychological or philosophical journal.
In short, I can remark that structure describes
the static side of an object and system stresses
the dynamic side, while hierarchy unites the
attributes of both. The concept of gestalt refers
to the syncretic level of mental activity and relates
more with the discordance function. The analytical
and synthetic levels can be, in a sense, associated
with Levels 2 and 3 in Fig.1.
17. Avdeev and Ivanov [3].
18. I have given them this name by analogy with speech;
however, this analogy goes much further than a simple
likeness. The formant structure is one of the most
trustworthy signs in image recognition and there are
some very general clustering mechanizms behind of it.
19. In reality, there is a hierarchy of labilities,
though most scales have too few zones per octave
for it to unfold itself in full.
20. A.Schoenberg, "Problems in Harmony,"
Persp. of New Music 11, No.2, 3-23 (1973).
21. Both "degree of a scale" and "step of
a scale" can be used in much the same way. The slight
difference is that "degree" mainly refers to a
scale zone, while "step" means the interval
between two adjacent degrees.
Euclidean space — similar to a Hilbert space,
but its basis contains only a finite number of vectors.
The components of the vectors are real numbers.
Fourier transform of a function — a function
that shows which rhythms constitute the original functions
and their relative contributions to it.
frequency — the number of oscillations per unit.
Frequency of a pure tone, for example, is the number of
density oscillations per second.
Gaussian distribution — the most important
probability distribution in mathematical statistics.
It is also called a normal, or standard, distribution.
Gaussian distribution is determined by two parameters:
the center (mean) and the dispersion (variance).
Figure 2a shows that for a Gaussian
distribution centered at the point hi the values
close to hi are most probable. The least probable
are the values lying farther than the dispersion of
the distribution from its center.
gaussoid — another name for Gaussian distribution.
Hilbert space — a mathematical object
representing a collection of all vectors that can be
constructed from the vectors of an infinite discrete
basis set. The addition of any two vectors of a
Hilbert space gives a vector of the same space;
the same holds for multiplication of any vector by
a complex number (having both real and imaginary parts).
Hilbert spaces are widely used in quantum mechanics
to represent the possible states of quantum systems.
invariant — a feature of a system that
remains the same after all transformations of a definite type.
maximum of a function — the point at which
the function's value is greater than the values of the
function for all arguments in a small region near the
point of maximum.
maximization — selection of the greatest
of all possible values.
minimum of a function — the point at which
the function's value is less than the values of the function
for all arguments in a small region near the point of minimum.
multidimensional space — a collection of vectors
that is characterized by several parameters (such as
length, width and depth in ordinary space, or the standard
hue/lightness/saturation representation of color).
one-dimensional space — a collection of vectors,
each of which can be determined by a single parameter
(such as time, duration or pitch).
overtone — a constituent of a musical sound
with frequency that differs from the frequency of the
principal tone by an integer factor.
pitch of a sound — the logarithm of the
sound's frequency. For complex sounds that consist of
many harmonics, pitch is associated with the frequency
of the principal tone.
principal tone of a musical sound — the
oscillation with the least frequency.
|