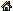IntroductionIn a previous paper [1], I outlined some of my ideas for a hierarchical approach to a theory of aesthetic perception. Applied to the perception of musical tones, this approach has led to a mathematical model based on the concept of information and some notions of quantum mechanics [2]. Within this hierarchical model, I have been able to define exactly what a musical scale is, so that the aesthetic potential of each scale can be inferred front a number of precalculated quantities. I concluded that there can exist only a discrete set of perceptible scales, any one of which implies a hierarchy of "embedded" scales, constituting a "tool kit" one has at hand when making music. Use of most scales is restricted by their limitations, though some of them contain subscales that might serve as musical modes or harmonies (chords). However, there are several universal scales (such as the well-known 12-tone equally tempered scale), which provide the most powerful support for both melodic and harmonic development. My findings indicate that any perception (including the perception of art) must be hierarchically organized, and that scale hierarchy can be considered perception's universal frame [3]. It is natural, therefore, to look for something like musical scales in arts other than music, and the first temptation is to find parallels to pitch perception in painting. What in a picture could be associated with musical pitch? There has been a long history of speculations on pitch-color correspondence, essentially growing from the simple relation of the seven notes to the colors of the rainbow. Bulat M. Galeyev has written an excellent review of such speculations, also providing an ingenious explanation of why the real correspondence between light and music cannot be found in such a straightforward way [4]. Although the correspondence may not be obvious, everybody feels that it does in fact take place and that painting can be readily associated with music, while other arts have some mysterious links to both. I cannot pretend to present a comprehensive aesthetic theory that would unite all the arts in a universal way. However, the hierarchical approach suggests a number of promising analogies between painting and music that take the problem in an unexpected direction. In this article, I present a general hierarchical theory of vision that could be applied to the perception of any visual form. For simplicity, I will refer primarily to painting; however, these references are intended to apply to any of the visual arts, including sculpture, architecture, dance, etc. The Basics of ViewingIn my search for the visual analogue of a musical scale, I follow some psychological considerations. The reader who is not too familiar with general psychology or is not interested in substantiation may skip this section, assuming on the basis of trust that there is some justification for the bold assertions that follow. Hierarchical ideas in psychology have found their most clear expression in A. N. Leontiev's theory of activity [5], which has become the paradigm for a vast psychological school. However, this theory has shared the destiny of many other conceptualizations, having been diversified by its followers to such an extent that they hardly understand one another. In order to fix the terms I will use, I have created a schematic display of the main notions of the theory (Fig. 1). There are three principal levels of generalization: activity, the highest level, consists of separate actions; action, the middle level, is in turn built of "elementary" operations. Subjectively, an operation — the lowest level — is performed "in no time" and can be thought of as a single moment of the pure (subjectively infinite) duration represented by an activity. Action occupies an intermediate position between these extremes: it spreads in time, but only within a limited range, from a beginning to an end [6].
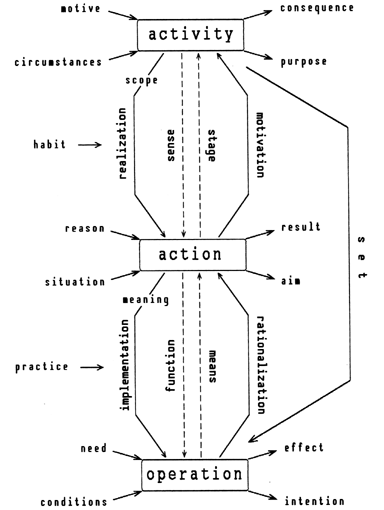
The distinction between activity, action and operation can never be absolute, since any operation may be unfolded further into a hierarchy of "suboperations" — in other words, the operation may become an action with respect to the suboperations; the former action then acquires a motivating power and becomes an activity. Inversely, a repeated action may fold into an operation; the embedding activity then turns into an action that has to be somehow motivated. Understanding these transformations requires the consideration of interacting activities, producing "shifts of consciousness" from one object to another. For my purposes, it is sufficient to note that human consciousness is generally focused on action, while operation and activity can be related to the two areas of the unconscious: the subconscious and the superconscious. The perception of sound as an activity can be called listening. Naturally, people listen differently in different circumstances and according to their perceptive habits. However, all kinds of listening are actualized in sequential actions of attending, that is, paying attention to one or another side of the sound. The operational form of sound perception can be called hearing. The same holds for the perception of any isolated characteristic of an integral sound. I distinguish, in particular, between levels of pitch listening, pitch attending and pitch hearing. Normally, the activity of listening to music proceeds on a rather high level, with pitch hearing completely enfolded within the smallest perceptible units of the music, which tend to be intonations, harmonies, or even textures or intonational planes. Nevertheless, pitch hearing cannot be dismissed, and its laws determine the development of the most abstract compositions. The complexity of pitch relations in music arises from the conception of an elementary (single) tone, characterized by its position on the logarithmic pitch axis, together with a margin of possible deviations that do not change the subjective perception of the tone [7]. In a laboratory experiment, it is possible to investigate the activity of determining the absolute pitch of a pure tone. Such determination can only be approximate, and the distribution of the estimates obtained in individual tests is close to the standard Gaussian distribution [8]. This "tone listening" folds into the hearing the harmonics of a complex tone, which, in its turn, is enfolded in the hierarchy of hearing a scale [9]. For visual perception, the obvious analogues of listening, attending an hearing are the activity of viewing, the action of looking and the operation of seeing. Given this analogy, the next obvious step is to find a kind of viewing similar to tone listening and to fold the subjective image obtained into an elementary conception. Which aspects of viewing could be correlated to pitch listening? Eventually one must choose between perception of form, size and color. Intuition rules out an analogy between pitch hearing and color viewing, because color specification requires at least three dimensions (such as hue, brightness and saturation; or red, green and blue) within a complex topology [10], so that the activity determining color appears rather unlike that of determining pitch. Comparison of a black-and-white reproduction to an original color painting seems to indicate that the function of color in painting may be similar to that of instrument timbre in music [11]. As for visual evaluation of size, it lacks one important feature of pitch hearing: there is no natural grouping of objects by their size that would have any universal significance. By contrast, for example, the overtone sequence naturally arises when a single tone undergoes a series of nonlinear transformations, an this discrete structure generally persists in further nonlinear processing (without accounting for redistribution between different harmonics). Similarly, we find that pitch scales are periodic, so that that two sounds are, in some way, the same when separated by an octave. Not so with the visual perception of the size of an object. As a rule, no "timbre" is associated with any definite size, and no evident periodicity is observed. In fact, size in visual art has much in common with the duration coordinate in music. That is why variations in size are widely used to express movement in painting [12]. Form viewing is the remaining option. Superficially, the vast variety of forms seems hardly reducible to a hierarchy of discrete scales. Nevertheless, I will try to demonstrate the similarity between visual form and musical pitch. Let us consider the perception of an angle on the plane. Just as the estimation of a musical interval implies a folded movement from one pitch to another (latent vocalization) [13], determining angles means internal transformation of one direction into another. This direction-determining activity is similar to pitch listening, having the same approximate nature and generating the same probability distribution as the internal representation of a single direction, characterized by its center angle and dispersion. I suggest also that angles are subjectively compared by their ratios. That is, the viewer tries to find how many times one angle is contained in another [14]. Mathematically, this means that a logarithm of an angle can/should be considered the additive measure of direction difference on the plane (i.e. the measure that can be obtained by summing up the measures of any partial intervals). Now, I can construct a series of "overtones" for a given angle j, considering angles nj, where for any integer n the resulting direction belongs to the same bundle of angles as the original one (the "principal tone" of the series). This "overtone series" of a plane angle seems quite natural when one accounts for the nonlinear (reflective) character of mental processes. If we assume that any operation is a folded activity, the implication is that there are many latent acts of mental reflection, so that an operation is multiply repeated inside the mind before it comes to actual performance. Thus, an angle is internally represented by the operation of building an angle of that size and producing a sequence of such angles, which constitute the angle's "harmonics". I consider a direction on the plane as the visual analogue of pitch, the difference between directions being the counterpart of a musical interval. Natural periodicity is self-evident: when a vector rotates around its starting point by 360°, it eventually returns to its initial position. I therefore conclude that the visual octave is the angle of 360° — or 2p radians. The mathematics presented in my earlier work [15] enters the game without any changes, and the conclusions reached by my previous study of hierarchical theory in aesthetic perception [16] could be reproduced here in every detail. Looking AroundI have supposed that angles on the plane are perceived in the same way as musical intervals are, and that the visual perception of size is to be associated with the perception of duration in music. Before tracing parallels between scale hierarchies in music and the visual arts, let us establish further analogies. The fundamental role of direction in the formation of visual scales may not be intuitively obvious. However, the more one looks at the idea of directional scales, the more attractive it becomes. Let us consider a curve on the plane (Fig. 2a). Though one direction continuously changes into another along the curve, it can still be thought of as a smoothed copy of a polygonal line (Fig. 2b). The smoothing is much like legato (or, sometimes, glissando) in music [17], and refers to the "manner of performance" rather than the "interval structure" of the curve. The discrete nature of direction perception becomes evident.
I propose that any curve is viewed as a sequence of "tones" (directions) of definite "duration" (lengths of the segments of the polygonal line). Thus, a correspondence between a musical intonation and a curve on the plane is established. For example, the curve shown in Fig. 2a,b might be notated as shown in Fig. 2c. The procedure is quite simple: the visual octave of 360° splits into 12 intervals of 30°, forming the 12-direction "well-tempered" scale. If I choose the left-to-right direction to represent do and the downward direction for la the rest of the scale can then be completely mapped accordingly, so that musical intonations can be "translated" into graphics, and vice versa [18]. This choice of "referent" directions requires a closer consideration. In pitch hearing, the la of the first octave proves a natural center due to the physical and physiological properties of human sound sensors. It seems therefore intuitively reasonable to associate la with the downward pull of gravity, which is perhaps the most important directional force for every living creature on Earth. Since the direction of do is to form a 90° angle with respect to la, (thus comprising three steps of the 12-tone scale), it is readily associated with the horizon line. However, here we must choose between the two possible directions this line can take: left to right or right to left. In the European tradition, proceeding from left to right appears to be preferable, while some other cultural traditions (e. g. the Arabic tradition) indicate a preference for proceeding from right to left. Cultural differences in perceiving graphic intonations would constitute the subject of a thrilling investigation. As a rule, the horizon line and the downward direction of gravity play a significant role in the arrangement of visual forms, which tend to align either horizontally or vertically. However, there exist compositions with a dominant slanting line. I suggest that the general alignment of visual forms correlates with tonality in music. Using the 12-direction scale introduced above, we can interpret Raphael's Madonna Alba (in which an ascending line at a 30° angle to the horizon dominates) is written in C-sharp minor, while Edgar Degas's Fin d'arabesque (which has an evident grouping along a line at 60° to the horizon) is in D minor. I will discuss the distinction between major and minor modes in the next section. Here is the point where an inexperienced reader becomes mystified. Why should one speak of any correspondence between pictures and music if the feelings excited by the curve in Fig. 2a have nothing in common with those called forth by the beautiful melody of "Green Sleeves"? The angles are not felt like music intervals, and we normally do not hear harmony in painting, but perceive it in some other way. I agree that painting acts upon us differently than music does, and this is why the two arts have been able to develop on their own, without too much interference. Still, this fact does not imply that intrinsic laws of aesthetic perception could not be the same in both cases. Ancient Greeks invented three different forces to explain the movement of the stars, the fall of a stone and the flight of an arrow. However, we know that all these movements are governed by the same Newtonian mechanics. The scent of a rose, the heating of a metal rod and the electric current in semiconductors, however different they may seem, obey much the same equations when it comes to mathematics. This is why I can say that plane curves are perceived in the same way as musical intonations are, though one cannot expect both perceptions to be identical in any respect [19]. Now, let the end of a curve come closer to its starting point (Fig. 3a). If the observer's perception is tuned to sizes much greater than the typical length of a segment within the composition, the curve is subjectively represented by a single conception (in the psychological sense explained in my earlier work [20]), and one sees a figure. In music, the simultaneous hearing of several tones produces the impression of a chord (Fig. 3b). It is well known that musical chords can easily unfold into specific intonations (arpeggio, latent polyphony, and the like), and there are theoretical grounds for thinking that all chords originate from folded melodic sequences [21]. In the hierarchical approach, such transformation from sequential to simultaneous form, and vice versa, is known as the process of refolding, and it is the refoldability of any hierarchy that enables it to reveal quite different hierarchical structures, depending on external situations. The particular case of a chord's rearrangement is widespread in music. The analogy with plane figures leads to the assumption that some figures could be considered refoldings of the same form, or different hierarchical structures produced by the same hierarchy (Fig. 3c). In general, the aesthetic significance of this community of forms in the visual arts cannot be overestimated. Through acquiring its own specific logic, art becomes a form of human thought.
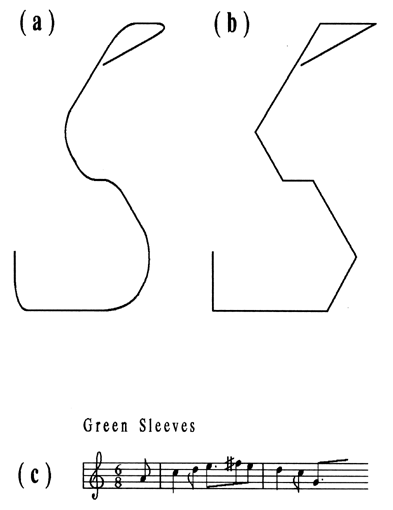
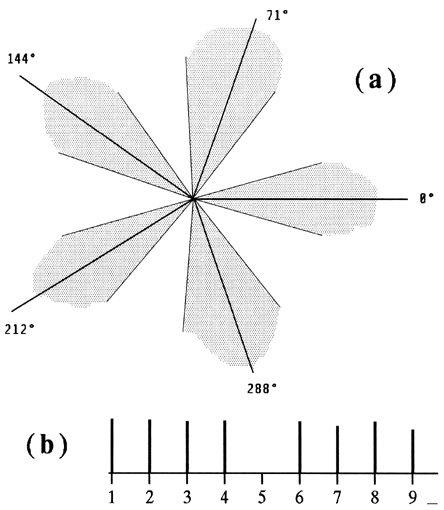
Because we can find analogues of melodic intonation and the chord in a plane curve and a plane figure, one can compare listening to music and viewing painting on a higher level, considering the interaction of an observer with a work of art as a whole. In general, the perception of a composition is a complex activity, starting with the formation of an overall impression and proceeding to more profound knowledge. A cursory glance at a picture or a single hearing of a musical piece gives an idea of its basic traits and fixes the crucial moments that will become centers of closer attention in further viewing or listening. Still more minute details come into view as the observer's acquaintance with the composition grows. Sometimes a fine detail induces the observer to change his or her notion of some global structure, though generally the first impression dominates. These sorts of changes in perception are examples of hierarchical refolding. In fact, the perception of a picture is not a momentary act. The observer's gaze jumps from one center to another, lingering just long enough to take in its surroundings and choose the direction of the next jump. In the most folded form, this process manifests itself as an alternation between fast, jerky eye movements (saccades) and slow, tremulous drifts — an alternation that could be considered the basic physiological mechanism of viewing [22]. In this respect, viewing a picture is very much like listening to music: whether it consists of harmonies or plastic forms, the whole is composed of a sequence of momentarily perceived portions. The artist intentionally controls this process, arranging figures in some deliberate order. A good composition generally compels the observer to reproduce the intended structure — although, naturally, individual peculiarities are necessarily present in each viewing [23]. "Standard" ways of dealing with objects one encounters in everyday life are built into standard ways of viewing common forms. This allows the artist to make control of the viewer's attention much more efficient. Realistic painting exploits these standard forms as a convenient background for expressive variations. Going DeeperNow I shall trace the analogy between pitch hearing and angle perception to more complex properties, which have been predicted by the mathematical model presented in an earlier work [24]. First of all, I wish to stress the importance of what I will call the "zone nature" of viewing angles, or the existence of a kind of angle interval within which all directions are perceived as functionally the same. This implies that any visual scale must be a collection of zones rather than single directions. The calculations show that all possible visual scales assume the division of the visual octave (the 360° angle) into a number of parts that is approximately an integer. Each division point marks a degree of the scale and is surrounded by a theoretically predicted zone. Any scale is characterized by its robustness index (a number between 0 and 1) and its regularity (the distinctness of the main scale). Briefly, robustness shows how the scale is preserved in numerous nonlinear processes in the brain. Low robustness means that the scale cannot become something subjectively significant, that it cannot be distinguished from the "mental background". Actually, each scale consists of a number of scale levels, embedded in some "main" scale (e. g. keys and chords in the 12-zone scale). Still, in "regular" scales, this main level always dominates, and the "notes" of the main scale are well separated from each other. Each possible scale is also represented by its "internal timbre", which is a set of amplitudes corresponding to the "overtones" of a specific direction (the integer multiples of the angle). It is the internal timbre that provides general information about the aesthetic potential of a scale [25]. For example, one possible scale binds five distinct directions together and corresponds to the pentatonic scale in music (Fig. 4a). This visual pentatonic scale has rather wide zones, its robustness is about 0.67, and its regularity value equals 1.42; the internal timbre contains 9 harmonics, but the amplitude of the fifth one is zero, so that there are two "formants" (1-4 and 6-9), with an equal number of components in each (Fig. 4b). The theory specifies that such a scale must be modally labile, which means that no one of the five directions can play the dominant role and become the key direction. The first ("harmonic") formant is too short to permit complex "chords" (figures): only one division of the whole angle is possible, at about 212° (the fifth; or 144°, the fourth). This explains why a "pentatonic" work of art masks complete forms, bringing forward the melodies of curves in continuous movement with no evident final point. One can readily find examples of this type of form in the art of China and Japan, in the bas-reliefs of the Hindu temples of the IX-XI centuries in Southeast Asia, or in the sculpture, of ancient Egypt [26]. The paintings of N. Rerikh (Men's Forefathers, The Himalaya, etc.) can serve as an example of modern pentatonic stylization.
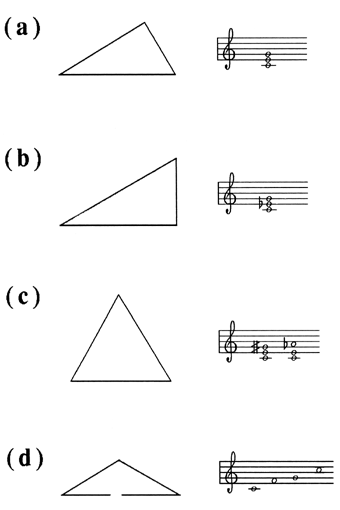
There are also many examples of the visual diatonic (the 7-tone scale). A comparison of the famous Venus of Milo with the Venus of Taurus shows that the former belongs to the higher stage of scale evolution, manifesting typically diatonic outlines with the elements of harmonic thought, while the latter is exclusively pentatonic. Consider also the paintings of M. Saryan, which demonstrate stylization according to the traditional Armenian diatonic, with the natural seventh. An instance of a universal visual scale is provided by the already mentioned 12-zone "well-tempered" visual scale, which is stable (harmonically, modally and chromatically), robust and regular. Just as the 12-tone scale is widely used in music, the 12-direction scale is widely applied in the visual arts. It permits the visual harmony of triads and uses a triangle as the base figure to build complex visual compositions. The angles of 90° (the minor third) and 120° (the major third) have been playing a significant role in painting for many centuries. Within the 12-direction scale, the visual triad is not a symmetrical (equilateral) triangle with equal 60° angles, but rather a right-angled triangle with complementary 60° and 30° angles. There are two "isomeric forms" of such a triangle, which cannot be transformed one into another by a plane movement (without mirror reflection); they correspond to the major and minor triads in music (Fig. 5a,b). The equilateral triangle corresponds to the sharp-looking enlarged triad, or to the chord with the small sixth instead of the fifth (Fig. 5c). This accounts for the dominance of asymmetrical compositions in painting, which are felt to be more stable and produce an impression of greater completeness.
Note that mirror reflection in the plane (or pitch axis) may drastically change the quality of an intonation. For instance, it may cause major triads to become minor and vice versa, which produces a rather unpleasant effect in tonal composition. This is why most arts tend to avoid mirror symmetry as soon as they develop out of the most primitive forms. However, mirror reflections are a standard trick in some branches of visual art (just as the inversion of a series is often used in serial music). It is my personal opinion that, apart from some expressive imitations of primitive art, such compositions demonstrate only a lack of integrity in scale hierarchy and a poor understanding of the internal relations between different elements of the composition, which is a result of the inadequacy of the material available. Architecture provides us with a clear example of persistent use of mirror symmetry, which for many centuries in this field has been considered an indispensable criterion of beauty. One factor contributing to the slow development of harmony in architecture was the relative difficulty or impossibility of grasping its products in a single glance. As a result, melodic impression dominates. Only in the twentieth century has the assimilation of new construction materials emancipated creative thought in architecture, and many bright asymmetrical works have come to light. Within the context of these new methods, the symmetrical compositions of former times can be treated as modal systems, allowing for a mixture of intonations of different quality in the same piece [27]. In ancient art, where pentatonic or diatonic form dominates, one does not find this harmony of triads. For example, the well-known Parthenon never violates the "complete and perfect system" of ancient Greek music. But a look at the architecture of classicist Paris (la Place de la Concorde, Versailles, le Palais de Justice, le Panthéon, l'église de la Sorbonne, etc.) is enough to provide an idea of how the conception of tonality can saturate the music of visual forms, even under the restriction of mirror symmetry! We can see that the typical classicist gable, for instance, follows the standard harmonic sequence tonic—subdominant —dominant—tonic (Fig. 5d). Visual MusicNaturally, pitch relations in no way exhaust the material of music, and it is not only sequences of directions that are registered in visual perception. In this section, I will outline several analogies concerning the correlations between different sides of visual imagery, leaving out the details. The visually perceived size of an object has already been compared to a note duration, so that a polygonal line immediately corresponds to a sequence of notes with specific duration and pitch. But this holds only for a plane curve, while the world around us is spatially organized. Sometimes, art ignores the dimensions of the real world in order to express the logic of a composition in a more abstract way. This is especially true of much modern art. In such cases, the analogy between visual forms and music is straightforward [28]. However, the visual arts are mostly inclined to the use of natural forms in artistically designed circumstances. The third spatial dimension is then modeled in painting using special techniques, the principal idea of which is to set up a number of visual planes differing by relative object sizes. As the size coordinate is related to time perception, a multiplane composition provokes a specific viewing sequence, generally starting with the front plane (the biggest objects), and moving deeper to the horizon line [29]. As plane angles change from one visual plane to another, the impression of polyphonic development appears. This is the most efficient way for an artist to control a viewer's perceptive processes and bring his or her ideas to an ordinary observer. Realistic art prefers contiguous movement in every "melodic" line (or polyphony — e. g. El Greco's The View of Toledo) or the harmonic support of a leading voice (homophony — e. g. Van Dyck's Rest on the Flight into Egypt: The Virgin with the Partridges). Modern art often resorts to sudden changes of harmonies and isolated intonations, with their peculiar expressiveness. Because the historical development of visual scales has always kept pace with the development of music, any historical pitch phenomenon could find its counterparts in the visual arts of the time. The transition from modal music to the conception of tonality brought many intermediate musical forms; the same holds for the painting and sculpture of the early Renaissance. The mystery of Leonardo's Gioconda may, in part, lie in the fact that the painting is made in a multiscale manner, with the body and hands of Mona Lisa performed in a mild pentatonic, while the face (including the smile) is exactly drawn in the E-major chord with a large seventh, violating the diatonic and making the chord an alloy of the major and minor triads (Fig. 6). Such chords sound rather dissonant, even in modern music based on the 12-tone scale. It is only in the 19-tone scale that the large seventh becomes consonant [30].
Another historical parallel arises between the introduction of the diminished-seventh chord in music and that of Cubism in painting, both occurring at the beginning of this century. The precise graphic analogue of the diminished seventh (do—mi flat—sol flat—si double flat) is a square, which has all the aesthetic potential of the musical chord [31]. Now, let us turn to the mystery of color, which for a long time had been a subject of abstract speculations and arduous controversy. I distinguish two aspects of any perception: perceptive quality and coloring. While quality determines what the thing is, coloring refers to details that do not carry the main idea of a composition and can be varied in different ways [32]. To be strict, I should point to a specific level of perception at which some components of the whole image are considered significant, while others are not. For instance, the instrumental cast for a musical piece may vary freely, allowing for numerous arrangements; however, in contrast to this potential for variation there is the composer's arrangement, which may often be specifically intended. In the same way, an artist may put his or her intimate thoughts and high symbolism into the colors of a painting, but a wider audience may well form opinions about it on the basis of a black-and-white reproduction; these opinions then occupy their own niche in the culture. On the other hand, one cannot apply color without form, just as there is no arrangement without something to be arranged. Even the most abstract play of colors or modulations of sound is somehow organized in space (or pitch) and this organization still obeys the logic of scale hierarchies. Naturally, there are cases when color cannot be detached from painting without qualitative changes, e. g. the landscapes of Claude Monet. By the same token, one cannot imagine Ravel's Bolero outside its arrangement for an orchestra. The links between impressionism in painting and music deserve deeper consideration than I can give them here. However, the principal idea of both is to shift attention to coloring, to make it play the role of perceptive logic. As a complement to the shift of coloring onto logic, pitch-like relations become highly coloristic, losing their qualitative aspect. However, they can never lose it completely, since an observer perceives any variation of color as a spatial form, and nothing can be perceived by sight that is not spatially organized. The role of color in visual arts is mainly to build forms [33], just as the primary role of an instrumental timbre in music is to mark a specific pitch. As W. Kandinsky noted, the boundary of two colors produces a form [34]. However, color is not the only way to produce visual forms. The same effect can also be obtained by light attenuation, sculptural techniques, use of the plasticity of the human body in choreography, etc. The variety of the visual arts comes forth in this range of possibilities. But the common feature of all visual arts is their basis in angle viewing, implying hierarchies of directional scales. Thus, there is a new language with which to speak of visual arts: that of scale hierarchies. There is, however, no need to measure angles when analyzing a painting, a sculpture, a gesture, etc. A little training gives one a sense of visual interval, just as we hear a musical fifth to be a fifth, and so on. As soon as such a sense is developed, one is able to appreciate the music of lines and discover a new world of visual aesthetics. Universal ScalingI have demonstrated how pitch-like relations generate scale hierarchies in both music and the visual arts. There are some indications that the same process takes place in poetry, but a more thorough investigation in this field is to be completed later on. It is my belief that hierarchical scaling and the potential for mathematical modeling that it allows provide us with a universal means of analyzing art. The application of the hierarchical approach to rhythm or nuances of performance requires somewhat different mathematics, but the work is in progress, and there is no doubt that some scaling phenomena are to be discovered there as well. One may ask, therefore, whether universal scaling in the arts displays only a peculiar regularity of aesthetic perception or manifests a more general law. I suppose that the grounds for aesthetic scaling are rooted in the hierarchical nature of human activity in general, which, in turn, reflects the inherent hierarchy of the world. Any creative impulse springs from some refolding of that hierarchy, and there is no purposeless art devoid of any objective necessity. Art is one of the means of joining individuals to society, and no artist creates anything purely for the sake of creation without regard for the opinions of potential observers. In any case, the artist is the first judge of his or her work and, as such, represents current societal attitudes. But any two individuals (even if one of them is a clone of another) can communicate only on the basis of some logic — in other words, a mode of activity brought to them both as a means of social regulation. Hierarchical scaling in aesthetic perception provides an example of such community. References and Notes1. P. B. Ivanov, "A Hierarchical Theory of Aesthetic Perception: Musical Scales". Leonardo 27, No. 5, 417-421 (1994). 2. L. V. Avdeev and P. B. Ivanov, A Mathematical Model of Scale Perception (Dubna, Russia: Preprint P5-90-4 of the Joint Institute for Nuclear Research, 1990) (in Russian). English version forthcoming in Journal of Moscow Phys. Soc. (1993). 3. Ivanov [1]. 4. B. M. Galeyev, Man, Art, Technology: The Problem of Synaesthesia in Art (in Russian) (Kazan: Kazan Univ. Press, 1987) (in Russian). 5. A. N. Leontiev, Activity, Consciousness and Personality (Englewood Cliffs, NJ: Prentice Hall, 1978). 6. In English, the difference between activity and operation corresponds, in a sense, to the difference between "doing" and "making". On the level of action, one finds verbs such as "perform", "fulfill", "undertake" and others describing the variety of possible conscious attitudes. 7. Ivanov [1]; Avdeev and Ivanov [2]. It is just this fuzziness of a single tone that accounts for the zone nature of pitch perception. Any perceptual structure must be a set of zone, and a signal is perceived as qualitatively the same while it varies within a zone. The possibility for such variation is the principal origin of intonational expressiveness, and different levels of music could not exist together without proper adjustment of intonation. 8. S. A. Helfand, Hearing: An Introduction to Psychological and Physiological Acoustics (New York: Marcel Dekker, 1981). 9. Ivanov [1]. 10. G. Wyszecki and W. S. Stiles, Color Science (New York: Wiley, 1967). 11. Ivanov [1]. See the related remarks in the previous section. 12. Another function of size in painting is to convey the impression of depth, which is similar to some uses of volume variation in music. Still, this "dimensional" function of size (or volume) is strongly correlated with movement from/to observer, and there is a simple proportionality between visual size and the time it would take for the observer to move away from the object by a distance corresponding to its size at some "standard" speed. 13. A. N. Leontiev, "The Biological and the Social in the Psychics of Man", in Leontiev, Selected Works Vol. 1 (Moscow: Pedagogika, 1983) pp.76-95 (in Russian); and "On the Mechanism of Sensory Reflection", Selected Works Vol. 2 (Moscow: Pedagogika, 1983) pp.6-30 (in Russian). 14. I consider the comparison by means of ratios a fundamental scheme for any measurement. The very idea of measure implies the "filling" of some interval with copies of a "unit interval". Since the internal evaluated need not be exhausted by an integer number of unit intervals, a special activity is required to fix the value exactly. That is why it would be subjectively easier to perceive integer ratios. The unfolding of this fixing activity is represented by be the notion of the fraction in mathematics. 15. Avdeev and Ivanov [2]. 16. Ivanov [1]. 17. Conversely, the aesthetics of rough angles is similar to that of staccato in music. 18. I speak of translating intonation because the transcription of complex musical compositions into figures would require a specially developed form of graphic notation that would allow for the arrangement of forms in perspective, the marking of boundaries between consecutive intonations and the adequate treatment of melodic jumps or nuances of performance. Such language can be developed along the lines of my theory, and its introduction in the arts may be just a matter of time. 19. However, it is possible to hear painting and see music; this form of perception is called synaesthesia, and can be developed with special training in folding the activity of comparison into the momentary (subconscious) operation. Synaesthetic perceptions are much more easily formed when the natural similarity of different perceptions is involved, and my theory predicts that angles may easily become heard as musical intervals as soon as the idea of directional scales occupies its place in modern culture. See also Galeyev [4]. 20. Ivanov [1]. 21. This process of intonational folding is evident in modern music, where a series can be represented in both melody and harmony. 22. D. Noton and L. Stark, "Eye Movements and Visual Perception", in Richard Held and Whitman Richards, eds., Perception: Mechanisms and Models (San Francisco, CA: W.H.Freeman, 1972). 23. I have chanced to take part in psychological experiments explicating the relations between the author's intention and the structure of viewing. A group of researchers studied creative perception of museum exhibitions and poetry using a specially developed technique. We proposed a formula to compare hierarchical structures and introduced a measure of perceptive integrity. The experiments have shown that the author's intention usually correlates with the structure of perception, though sometimes the realization of this intention lacks due integrity. The experimental procedure and the results have been described in two unpublished manuscripts: V.V.Koren, A Hierarchical Analysis of Museum Exposition (Moscow, 1983); V.V.Koren, The Hierarchical Approach in the Psychology of Creativity (Moscow, 1984). 24. Avdeev and Ivanov [2]. 25. Ivanov [1]. 26. There is profound integrity in the art of every nation at any time. Pentatonic music lives together with pentatonic visual arts; when another scale appears in one kind of art, it quickly penetrates all the other branches. Human society is developing as a single organism; the basic cultural traits of any stage of this development constitute a cultural formation that exists in contrast and as a complement to the current economic formation. 27. I am grateful to E. Sidorkina for the ideas expressed in this paragraph. 28. L. Avdeev has offered the excellent example of Joan Miro's The Dancing Party in the Princess' House, which perfectly reproduces the nature of rock music: pentatonic intonations on a hard background of chords. 29. See also the recorded viewing routes in Noton and Stark [22]. 30. Ivanov [1]. 32. Ivanov [1]. 33. Actually, color can also perform the function of texture indicator, but an exploration of this function would lead us to comparison with other sensory modalities (touch, smell, etc.). 34. W. Kandinsky, Concerning the Spiritual in Art (New York: Dover, 1977).
|