Нечеткие множества и релятивистское сложение скоростей

Аксиоматический каркас для пересечения i(a, b) и объединения u(a, b) нечетких множеств задают следующим образом:

1. граничные условия:

2. коммутативность:

3. монотонность:

4. ассоциативность:

Вообще говоря, объединения и пересечения нечетких множеств не идемпотентны. Любой выбор общего вида объединения и пересечения будет так или иначе нарушать какие-то свойства булевых решеток. В частности, могут не выполняться закон исключенного третьего и закон противоречия.

Как известно, условия 1–4 приводят к неравенствам

,

так что  i(a, b) < u(a, b)  для  a ≠ b . Дополнение нечеткого множества чаще всего определяют как c(a) = 1–a.

Можно предложить пример, показывающий, что аксиомы 1–4 могут быть несовместимы с правилами Де Моргана:

Действительно, сопоставим каждому элементу x_i нечеткого множества вещественное число , такое, что

.

Когда χ пробегает значения от –∞ до +∞, μ монотонно возрастает от 0 до 1. Сконструируем дополнение A согласно общему правилу:

.

Наконец, определим пересечение двух нечетких множеств как

.

Это выражение удовлетворяет граничным условиям для пересечения, оно очевидным образом коммутативно и монотонно. Прямым вычислением можно показать ассоциативность:

.

Так определенное i(μ₁, μ₂) не идемпотентно, хотя можно видеть, что оно асимптотически идемпотентно при χ → ±∞, что обеспечивает правильный переход к обычным (не нечетким) множествам.

Воспользуемся теперь правилом Де Моргана, чтобы определить объединение множеств через пересечение и дополнение:

Поскольку определенные таким образом объединение и пересечение совпадают, объединение не вписывается в аксиоматический каркас, ибо нарушаются граничные условия при  μ₁ = 0  и  μ₂ = 1 . И, конечно же, величина  i(μ₁, μ₂)  никак не может быть меньше u(μ₁, μ₂), как это следовало бы из базовых аксиом. Заметим, что при таком выборе пересечения и объединения нарушается закон исключенного третьего и закон противоречия, ибо

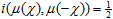
Физический смысл этих определений — релятивистское сложение скоростей. Частицам, движущимся вперед со скоростью света, приписано значение μ = 1, а тем, что движутся со скоростью света в обратном направлении, — значение μ = 0. Если ограничиться при сложении скоростей только положительными значениями, объединение относится к так называемому классу Гамакера с γ = 2:

Вместе со стандартным дополнением оно порождает пересечение

,

удовлетворяющее и аксиоматическому каркасу, правилам Де Моргана. Однако в этом случае определение дополнения оказывается «физически несовместимым» с определением объединения, поскольку галилеево правило сложения скоростей используется вместе с релятивистской формулой.

14 мая 1997