The Straights of the Circle

Unless a person grows into a mathematician, everybody intuitively feels the presence of two opposite sides in any activity: we either proceed stage by stage from one goal to another or repeatedly reproduce the same something, intentionally abandoning the balance to regain it in a little while. This could metaphorically be pictured as the contrast of the straight line and the circle, of translation and rotation. Of course, any reproduction implies production (since one needs at least to do something, to redo it), as well as production is impossible without reproducing the productive environment, the basics of technology (including the typical operations). However, at any instance, identity builds up at a higher level, compared to thus lifted distinction; there are numerous transitions of one thing into another that allow us to establish the unity of the different as a kind of generalization (cultural assimilation). When mathematics sets to ignoring such (qualitative) distinctions in favor of sheer quantitative analysis, logical fallacies are bound to creep in.

Just a simple example. From high school maths, we learn that any periodic (say, with the period 2π) function can be expanded into a Fourier series:

,

with the coefficients evaluated as

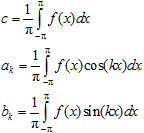
he constant c is commonly considered as a special case of the coefficients a_k , stressing the fact that the expression to compute c = a₀ can be obtained from the equations for a_k just formally setting k = 0. Everything looks hard and fast, at first glance. Still, there is a minute nuisance: why should we supply the constant term of expansion with a factor of 1/2? To keep uniformity, we should rather start with a uniform expansion like

,

taking into account that , and hence the value of b₀ is arbitrary (which, by the way, is annoyingly suspicious too)? Yes, we have to introduce an "extra" quotient in the integral for a₀; but why in heaven should we aim at the similarity of formulas for series coefficients instead of original series uniformity? Students are not allowed to ponder much upon such questions; at exams, they must report what they have been taught. Working mathematicians would shyly sweep the doubts under the carpet, with a vague reference to the centuries-old tradition. Still, we perfectly know that new prospects of research were always found where people tried to grasp the meaning of some strange arbitrariness: apparently, one can do either that way or another; later on, one becomes aware of the principles of choice and can consciously act according to practical needs. For a well-known example, take the story of the Euclid's postulate of parallels. Or Archimedes' findings. The stray one-half factor in the theory of Fourier expansions may well happen to be of the same crew.

In the preliminary approximation, the constant term of the series is very like an integration constant. It is well known that an indefinite integral is a family of antiderivatives, with the choice of any particular member depending on the additional (initial, boundary, asymptotic...) conditions which do not follow from the properties of the integrand. Well, here is the truism about the integral as a kind of sum, with Fourier series becoming Fourier integrals etc. Let's be less primitive and never agree to the candy box without the candies. It's high time to dig a little bit deeper.

One could try to ponder on the qualitative distinction of variables from constants: the former are meant to change, that is, to depend on something. A constant does not depend on anything; at most, it may vary along the lines irrelevant for the issue in question. When we hear the common objection that a constant can be considered as a special case of variable, namely, a variable that always takes the same value, this is no serious discussion but rather resembles the old pun of the former soviet dissidents: the Party's line is straight; it bends at any point... In fact, all mathematical trickery with identifying qualitatively different things exploits a few banal logical fallacies known from the most ancient history. For instance, as soon as we admit that a constant is just a constant-valued function, we still have to explain what we mean by "constant-valued". That is, to define a constant as a function, we need to have an idea on constancy (identity) as such. This is a typical case of logical circularity. In that way, one does not eliminate the opposition of constancy and variability, but rather shoves it aside, hanging it up to somebody else's hook. Just we do attaching the one-half factor either to the constant term of the Fourier series or to its integral expression. In other words, a constant is something that remains the same all the time, and it is not like a periodic function that does not only regularly reproduce the same value, but also is meant to regularly deviate from that value; otherwise, it has no opportunity to come back.

To summarize, the introduction of a constant term in trigonometric series contradicts elementary logic and violates the "natural" structure of the series (as a span over an orthogonal basis). As there is no need in such a "zero" term, its particular form is out of the question. Of course, one is free to evaluate the difference of one function from another; sometimes, this difference may be reduced to a mere constant. However, nothing hinders adding to the sum of a trigonometric series any function at all, provided it takes equal values at the ends of the segment [–π, π], or even diverges there, but "in the same manner". Such a background dependence can play the role of the "zero" term no worse than mere constant; moreover, in certain cases, splitting a function into two (not necessarily orthogonal) dependencies may be preferable from the "physical" viewpoint, stressing the objective structure of motion, its hierarchical nature. Obviously, we do not need any uniformity of the background function with the formulas for the Fourier series coefficients; they refer to different entities.

In general, we can split any function (not necessarily periodic) into a sum of the "periodic" and "non-periodic" components: the former is obtained as a sum of a Fourier series; the latter plays the role of reference level for any oscillations. Obviously, the "non-periodic" component, in its turn, may exhibit certain oscillatory behavior; however, the characteristic periods of such oscillations will normally be rather large, on the scale of the earlier established periodicity, so that all the "local" oscillations will average into zero during one higher-level period. In this way, we unfold a hierarchy of oscillatory motion, and it is only in very special (practical) cases that it can be reduced to something planar. It is also evident that every such hierarchical structure can be folded and unfolded into a similar structure with different sequence of levels, which, too, is determined by applications rather than purely mathematical necessity. Eventually, we come to considering various ensembles of the possible hierarchical structures as virtually co-existent; this will shift the focus from the details of inner motion onto its global organization, picturing the hierarchy as a whole, a unity of all its special positions.

Returning to the metaphor of the circle and the straight line, we find that, at each point of the circle, the motion has a definite direction represented by a straight line; still, any physicist knows that such ("virtual") displacements lie in a different (tangent) space, and we cannot arbitrarily identify the points of the configuration space with momenta. Similarly, one can "straighten" a circle representing it with a sequence of small segments of a straight line. However, such a picture is only acceptable where the difference is practically irrelevant; formally, the indication of the adopted scale (the level of consideration) is referred to as convergence to a limit. That way or another, the removal (lifting up) of the opposition is a quite real operation; once we forget it, we get stuck in logical problems.

By the way, a few words about symmetry. To be honest, is nothing like identical zero, so that omitting the terms with b₀ in the Fourier expansion is only possible in a limited area. Proceeding to infinity, we come to an indeterminable form of the type , и далеко не факт, что при ее раскрытии получится ноль. Когда студентам говорят, что , and it is not at all evident that it will always evaluate to zero. Students are often told that a trigonometric series is defined in the interval (–π, π); this is a deliberate fraud, since both the sine and the cosine are defined for any real numbers, and hence the sum of the series will exist everywhere. It's quite another matter that the sum will necessarily be periodic in the absence of "zero" components, which are the only way to explicitly introduce any trends, albeit reducible to mere constant shift. In other words, periodicity is an entirely local phenomenon (since we compare the states of the same object, the time points); in infinite domains, it may become just anything. From everyday practice, any programmer learns that the sine and the cosine are only reliably computable for relatively small arguments; the reduction of very big numbers to a standard interval leads to a significant loss of accuracy.

There is a much more fundamental reason to omit the "zero" terms in Fourier series. To the matter of fact, zero is not entirely a number. Indeed, it is not a number at all. It is merely a common notation for the limit process, a placeholder for the (vaguely felt) boundary of the applicability area. To include zero in the set of natural (or real) numbers is, for a person of reason, an act of violence against logic.

In any mathematical (or any other) theory, zero denotes the absence of the object (or an effect), that is, passing beyond the object area. Formal extrapolation of a theory beyond its applicability region is not always justifiable. Infinity says about practically the same: here, we take the object area as a whole as a specific (higher-level) object that is different from any object belonging to the theory's domain. Conversely, zeros refer to the lower levels of hierarchy taken as a whole. Due to hierarchical conversion, the distinction of the "upper" and the "lower" is relative; that is why, in formal theories, zero readily tends to produce infinities, while infinity get inverted into zero.

In a sensible (logically consistent) theory, the natural number sequence starts with unity; this is the first natural number (indicating the presence of something to count al all). Zero is not a natural number, as it is just a contracted notation for not belonging to the set of natural numbers. In the same manner, we can only speak about trigonometric series when we get at least one trigonometric function; adding non-trigonometric terms drives us beyond the theory of trigonometric series to a different theory (if not to an eclectic mixture of theories). Similarly, in power series expansions, the "zero-order" term is nothing but a reference to outer conditions, the other levels of hierarchy; anyway, this is beyond the strictly understood object area. Considering a problem "in the zero order", we, in fact, do not consider it at all, rather preparing the very possibility of consideration by preliminarily outlining the object area; it is after this preliminary work that we can proceed to discussing the object in first order, adjusting the details at higher levels.

At school, we learn about various smart "theorems" concerning the convergence of trigonometric series. For instance, it is said that a continuous function in the segment [–π, π] with no more than final number of extremums has a Fourier expansion that will converge everywhere in this segment, so that the sum will coincide with the function's value in every inner point, while at the both ends of the segment, the series will evaluate to

,

The typical school example is linear dependence f(x) = x, with the Fourier transform, for convenience, reduced to the interval (–1, 1), given by

Formally substituting , we obtain (with the epithet "evidently") that every term of the series identically equals to zero; on this reason, we dare to conclude that the whole sum will also compute to zero, thus brilliantly confirming our rule about the ends of the segment... In reality, this derivation contains an elementary logical fallacy; normally, students get punished with poorer marks for such blunders at exam. Indeed, the terms of the series are only equal to zero at for finite k; in the limit, however, we come to the familiar indeterminable form of the type , which has to be honestly analyzed and brought to a specific value. The superficial decrease of each term as the inverse of the index is bluntly compensated by the increasing number of terms, so that here, as well, there is no loophole for trickery.

Surely, this is not an incidental lapse of reason; in fact, we speak about a most profound logical problem. Conventionally, one might call it the substitution principle. Mathematicians suppose all the way that one can (at least in principle) to substitute any term in any formula with anything else, and nothing will change. As we observe, this does not always hold. In general, one cannot evaluate an infinite sum substituting some specific value for the parameters (arguments) in every single term of the expansion. The trick will work under certain conditions. However, in real life, the result of a substitution often depends on its practical realization (for instance, on the order of substitution and the technique of producing the partial sums). For recursively-defined formulas, momentary substitution becomes utterly meaningless; any operation must refer to a specific stage of recursion. Well, the bulk of problems arising from the substitution principle deserves a separate discourse.

Now, what are the limit values of a Fourier series at the ends of the one period-long segment? A catchy question. Yes, one could simple abandon the idea of computing the sum at the ends and believe that the limit at does not exist, so that only the inner points in (–1, 1) are legal. Just to lull one's conscience, the single-ended limits could be considered. However, this is no bright perspective, is it? Let us, instead, look closer to the graphs of the partial sums of the trigonometric series:

Here, it is literally evident that every partial sum is representable with a smooth curve, and there is no reason to expect any discontinuity in the infinite limit. Anybody alien to mathematics will say that the graph will "topologically" converge to the polygonal line:

Yes, this function is not single-valued, and the arguments map to a continuum of ordinate values. Still, who can prevent us from slightly rotating the axes, to arrive at perfect unambiguity? Geometric forms do not depend on the method of their arithmetization. The curve (trajectory) remains the same geometrical entity however parametrized. It is the forms of representation that change, but not the represented objects. The converse holds as well: the same numerical structures can correspond to very different objects (which may be very far from mathematics in real life). Any representation is conventional, partial, and valid within a particular approximation (in a specific context). Still, at least some representation is always possible and practically inevitable.

By the way, the trick with the displacement of the coordinate system axes is not new: thus, in complex analysis, we have long since grown accustomed to such manipulations in the vicinity of pole singularities. So, should we be any shyer with Fourier expansions?

It is important that the Fourier series for any "decent" function f(x) will converge to some continuous (and, of course, periodic) function F(x), which, in general, does not need to coincide with f(x). To eliminate the formal "leaps" at the ends, one could resort to a parametric form of the incident function (say, with the path length as a parameter):

In this representation, there is no longer any discontinuity, and the apparent "leaps" get "filled" in a natural way, without special effort. However, one still cannot get rid of the problem: with more terms in the expansion, the sum will rapidly oscillate (albeit with a quickly decreasing amplitude), so that evaluating the limit is not quite trivial; instead of the indefinite terms of the type at the ends of the segment, we get the same indeterminacy in every inner point! To separate the trend from variations, there is a standard trick: we "smoothen" the curve, eliminating too fast oscillations:

The oscillations with the periods much smaller than Δx will gracefully average to zero, thus producing a "good", smooth curve. With more terms in the Fourier expansion, the averaged function will converge to the same limit F(x), without annoying indeterminacies. Still, in some cases, it is the deviations from the average that are of primary interest. The theory of scaling in music provides a practically important example.

The Dirichlet theorem could be discussed in exactly the same lines. Thus, from the graph for a partial sum of the Fourier expansion for the function sgn(x)

we, once again, perceive convergence to a polygonal line, with the discontinuity of the original function filled in the limit by a vertical segment of the ordinate axis. Instead of a single leap, we get a continuous meander. And this is right, since the sum of periodic functions with commeasurable periods is a periodic function; and we expect it like that, intuitively opposing the straight line and the circle as qualitatively different forms of motion. A graph of a periodic function is a sort of involute of a circle (or many circles) along a chosen line.

Despite the formal convergence of a trigonometric series within a finite interval, we cannot say that it will converge to the incident function. The minute details of the hierarchy (in particular, the hidden behavior of the partial sums) are in no way lost in the result. That is why it is not always reasonable to compute a function using its Fourier expansion. And it is not the matter of slow convergence or apparent singularities. Any science speaks about things outside us (however preconditioned and intertwined with our material activity); so, the structure of science must correspond to the structure of its object. Where the very organization of human activity prescribes the usage of Fourier analysis, we must employ it, abandoning the hope to simplify things with apparent principal trends or global features to suppress less important variations. For example, if a linear function or a step are produced by some electronic devices, the wave nature of the process will practically manifest itself one way or another; here, trigonometric expansions are all right. On the contrary, considering a technological process, an evolution of a star, or a banal movie show, we find a linear approach (though, possibly, accounting for various reflective loops) more natural and self-suggesting. The opposites do not exist one without the other; all we need is to seek for the right place for everything.

Well, the notion of a limit (including the limit of a series or an integral) is not as trivial as it may seem from the school course of mathematical analysis. We have to consider convergence of an object to an object, rather than mere numerical convergence (which, however, may be an important special case). A function can be arithmetized ("computed") in many ways; no single arithmetization will express the idea of the function as such. Our examples of "topological" (or "extensional") convergence are in no way a complete enumeration; they merely stress the difference of the operational definition of a function from its extensional definition (a "graph"). There are many more types of definition (like implicit, schematic, illustrative, applied) that cannot be reduced to neither operations not sets. The hierarchy of all the possible definitions is a function proper.

It is self-understood that any revision of the notion of the limit will introduce certain specifications to the theory of differentiation or integration. No serious shock for the whole of mathematics, of course; still, it may be useful to cast a fresh glance to an old moss-grown domain.

In a specifically practical aspect, the idea of a graphic limit may be of value where the traditional approach states the absence of a limit or suggests an arbitrary closure. It is quite possible, that, in such cases, there is no arbitrariness at all, and the apparent lack of convergence is due to a poor parametrization. One could informally conjecture that all the known "exotic" functions are nothing but examples of inconsistent (unnatural) arithmetization; with a more sensible approach, all the uncommon features will disappear, and everything will get back to the combination of the two simple types of motion: the straight line and the circle, translation and reflection.