Прямая и круг

Пока человек не стал математиком, он интуитивно противопоставляет две стороны всякой деятельности: либо мы продвигаемся поэтапно от одной цели к другой — либо многократно воспроизводим одно и то же, уходя от равновесия — и возвращаясь к нему. Метафорически это можно мыслить как противоположность прямой и круга, поступательного движения и вращения. Конечно, воспроизводство предполагает производство (чтобы сделать нечто заново, надо его, как минимум делать), а производство опирается на воспроизводство производственных условий, технологические стандарты (типовые операции). Но тождество возникает каждый раз на ином уровне, нежели различие, и устанавливается путем обобщения (культурной ассимиляции) многократных переходов одного в другое, как единство различного. Когда математика игнорирует подобные (качественные) различия и пытается все свести к чисто количественным соотношениям, возникают логические неувязки.

Простой пример. Из школьного курса анализа мы узнаем, что всякую периодическую (для определенности, с периодом 2π) функцию можно представить рядом Фурье:

,

коэффициенты которого вычисляются по формулам

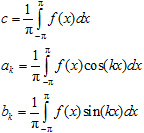
При этом постоянную c обычно считают частным случаем коэффициентов a_k , подчеркивая, что формула для вычисления c = a₀ получается из формул для a_k формальной подстановкой k = 0. На первый взгляд — все железно. Только не дает покоя одна маленькая странность: с чего бы вдруг нам приходится пририсовывать к этому члену разложения множитель 1/2? Коли уж блюсти единообразие, так почему бы не написать с самого начала:

,

учитывая, что 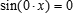, и потому значение b₀ может быть произвольным (что, кстати, не менее подозрительно само по себе)? Разумеется, при этом появится "лишний" множитель перед интегралом для a₀ — но почему мы должны добиваться одинаковости формул вычисления коэффициентов, а не универсальности ряда? Студентам над такими проблемами размышлять не по чину — им надо на экзамене отвечать, как предписано. Работающие математики стыдливо заметают вопрос под ковер, ссылаясь на историческую традицию. Но мы-то знаем, что в истории математики новые направления исследования возникали именно там, где люди задумывались над природой необъяснимого произвола: можно так — а можно и по-другому; потом выясняется, в каких случаях надо так, а в каких по-другому. Взять хотя бы пресловутую аксиому о параллельных. Или деяния Архимеда. Блуждающая половинка в теории рядов Фурье вполне может оказаться из той же компании.

В первом приближении: постоянный член разложения очень напоминает постоянную интегрирования. Известно, что неопределенный интеграл дает семейство первообразных, и выбор какого-то определенного представителя этой семьи связан с наложением дополнительных условий (начальных, граничных, асимптотических, ...), с подынтегральным выражением никак не связанных. Напрашивается ходячее сравнение суммы с интегралом, переход от рядов к интегралам Фурье и т. д. Но это как-то уж очень примитивно, и мы на фантик не поведемся. Будем копать глубже.

Попробуем зацепиться за качественное различие: переменные величины отличаются от постоянных тем, что они меняются — то есть, от чего-то зависят. Постоянная не зависит ни от чего — в крайнем случае, от чего-то совсем другого, из другой деревни. Когда нам возражают, что постоянную можно рассматривать как частный случай переменной (принимающей все время одно значение), — это больше напоминает не серьезное обсуждение, а известный советский анекдот: линия партии прямая — у нее в каждой точке перегиб. По факту, математические фокусы с отождествлением качественно различных вещей всегда опираются на пошлые логические ляпы, знакомые всем с ранней античности. Например, в данном случае это логический круг: ну хорошо, пусть постоянная — тоже функция, только принимает она всегда одно значение; но откуда нам известно, что это значение только одно? То есть, чтобы определить постоянную как функцию, мы должны уже иметь представление о постоянстве как таковом. Несовпадение постоянства и переменности таким способом не устраняется, а лишь задвигается в другое место — совсем как с блуждающей половинкой в тригонометрических рядах. Другими словами, постоянная — это именно постоянная, а вовсе не периодическая функция (для которой важно не только возвращение к тому же значению через определенный интервал, но и факт регулярного ухода от этого значения — иначе просто неоткуда возвращаться).

Следовательно, введение постоянного члена в тригонометрические ряды идет вразрез с элементарной логикой, со строением ряда (сумма по базису ортогональных функций). Не должно там быть никакого "нулевого" коэффициента — и вопрос о его форме просто не возникает. Разумеется, мы можем оценивать отличие одной функции от другой — и в каких-то случаях свести его к числу. Но ничто не мешает нам вместо постоянной добавить к тригонометрическому ряду любую функцию, принимающую одинаковые значения на концах промежутка [–π, π], или даже расходящуюся в этих точках — но "одинаковым" образом. Такая добавка ничем не хуже константы может играть роль "нулевого" члена ряда, а в каких-то случаях такой выбор предпочтительнее, поскольку он может подчеркнуть "физику" дела, характер движения, его иерархичность. Понятно, что говорить о единообразии формул для коэффициентов ряда и для "нулевого" члена уже никак не приходится.

В общем случае, мы можем представить произвольную функцию (уже не обязательно периодическую) в виде суммы "периодической" и "непериодической" компонент: первая получается суммированием ряда Фурье — вторая играет роль фона для осцилляций. Понятно, что в "непериодической части" можно также усмотреть "периодические" компоненты — но с очень большим (по шкале ранее выявленной периодичности) периодом, так что на каждом периоде более высокого уровня все "локальные" колебания успевают много раз усредниться в нуль. Так возникает иерархическая структура колебательных движений — и сводить ее к чему-то плоскому допустимо лишь в особом (практическом) контексте. Ясно также, что любую такую иерархию можно свернуть — и развернуть в нечто подобное, но с другим набором уровней. Это, опять же, определяется не математикой, а ее приложениями. Наконец, можно рассматривать ансамбли возможных иерархических структур как виртуально сосуществующие; внимание при этом переносится с деталей внутреннего движения на его глобальное строение, на черты иерархии как таковой, в единстве всех ее частных структур.

Возвращаясь к метафоре круга и прямой, мы вспоминаем о том, в каждой точке круга движение направлено по прямой — но физики знают, что такие "виртуальные" смещения лежат в другом (касательном) пространстве, и безоговорочно путать координаты с импульсами нельзя. Точно так же, можно "спрямлять" круг, представляя его суммой малых отрезков прямой, — но такое представление приемлемо лишь там, где различие практически несущественно; формально указание такого масштаба (уровня рассмотрения) называется предельным переходом. В любом случае, снятие противоположности есть вполне реальная операция; стоит об этом забыть — и логические проблемы неизбежны.

Кстати о симметрии. По-честному, вовсе не тождественно равняется нулю, и говорить об отсутствии в разложении членов с b₀ возможно лишь в ограниченных областях. При уходе на бесконечность мы получаем неопределенность вида , и далеко не факт, что при ее раскрытии получится ноль. Когда студентам говорят, что тригонометрический ряд определен в интервале (–π, π), — это жульничество, ибо синус и косинус формально определены на всей числовой оси, и сумма ряда должна существовать всюду. Другое дело, что при отсутствии "нулевых" компонент сумма неизбежно окажется периодической функцией — и придать ей хоть какую-то непериодичность (хотя бы простой сдвиг) возможно только путем явного введения непериодических членов в разложение. Иначе говоря, периодичность есть принципиально локальное явление (поскольку мы сопоставляем состояния одного и того же объекта, два момента времени); в неограниченных областях она может превратиться во что угодно. Чисто практически, всякий программист знает, что синус и косинус реально вычислимы только при относительно небольших значениях аргумента; приведение их к стандартному интервалу для больших аргументов связано с заметной потерей точности.

Для того, чтобы отказаться от постоянного члена в тригонометрических рядах есть и более глубокие основания. Дело в том, что нуль — не совсем число. И даже совсем не число. Это обозначение перехода к пределу, указание на порог применимости. Включать нуль в состав натуральных (или вещественных) чисел есть, для разумного человека, насилие над логикой.

В любой математической (и не только математической) теории нулем обозначают отсутствие объекта — то есть, по сути, выход за границы предметной области. Формально применять теорию вне области ее применимости — это не всегда полезно. Бесконечность — другое обозначение того же самого, когда мы рассматриваем предметную область теории целиком как особый объект, отличный от любого объекта из предметной области (более высокий уровень иерархии). Обратно, нули появляются там, где мы говорим о нижележащих уровнях, взятых как целое. В силу обращаемости иерархий, различие "верха" и "низа" относительно, и потому в формальных моделях нуль так легко превращается в бесконечность, и наоборот.

В осмысленной (логически последовательной) теории натуральный ряд начинается с единицы — это первое натуральное число (указание на присутствие чего-то, что можно считать). Ноль натуральным числом не является, это лишь сокращенная запись непринадлежности классу натуральных чисел. Соответственно, суммировать тригонометрические ряды мы имеем права только с тех членов, где реально появляются тригонометрические функции; в противном случае это уже не тригонометрический ряд, а нечто эклектическое. Точно так же, и в степенных рядах нулевой член — ссылка на внешние условия, другие уровни иерархии — выход за рамки предмета. Рассматривая что-то "в нулевом приближении", мы фактически не приступаем к рассмотрению, а пытаемся очертить границы рабочей области, чтобы потом уже предметно обсуждать вопрос в первом приближении и уточнять детали в высших порядках.

О сходимости тригонометрических рядов доказывают всяческие умные "теоремы". Так, например, утверждается, что если функция непрерывна на [–π, π] и экстремумов у нее не более чем конечное число, ряд Фурье для этой функции сходится всюду; внутри интервала (–π, π) сумма ряда в каждой точке совпадает со значением функции, а на концах отрезка мы получим одинаковые значения

,

Типичный школьный пример — линейная функция f(x) = x, Фурье-разложение которой, для удобства приведенное к интервалу (–1, 1), имеет вид

Если формально подставить , обнаруживаем (с прибавлением: "очевидно"), что каждый член ряда тождественно равен нулю, а потому, дескать и сумма ряда будет нулем, так что наше правило относительно концов отрезка, вроде бы, блестяще подтверждается... На самом же деле, в рассуждения вкралась элементарная логическая ошибка — студентам за такое снижают балл на экзаменах. Действительно, равенство членов ряда нулю имеет место только при конечных k, а в пределе мы имеем уже знакомую неопределенность вида , которую надо честно раскрывать и выяснять, куда все в итоге приползет. А убывание каждого члена обратно пропорционально индексу тупо компенсируется увеличением количества членов — и здесь сжульничать тоже не получится.

Речь идет, конечно, не о единичном прегрешении против логики — тут глубочайшая логическая проблема. Условно можно было бы назвать это принципом подстановки. Математики сплошь и рядом предполагают, что в любой формуле возможно заменить любой терм на что-нибудь другое — и ничего не изменится. Как мы видим, это не так. Нельзя оценивать значение бесконечной суммы, подставляя какие-либо значения параметров (аргументов) в каждом из ее слагаемых по отдельности. Такой прием срабатывает лишь при определенных условиях. В реальной жизни результат подстановки часто зависит от способа реализации — например, от порядка подстановки и метода получения частичных сумм. Если формула задана рекурсивно, говорить о единовременной подстановке термов вообще невозможно — такая операция может иметь смысл только на одном уровне рекурсии. Но эта проблематика — для особого разговора.

Так чему же равны пределы на концах отрезка? Вопрос на засыпку. Можно, конечно, отказаться от сильных утверждений и заявить, что предела не существует, и следует ограничиться только внутренними точками интервала. В крайнем случае, прикрутить односторонние пределы. Но это скучно. Давайте пристальнее посмотрим на график частичной суммы ряда:

Тут уже в буквальном смысле очевидно, что каждая частичная сумма представлена гладкой кривой, и что нет ни малейшего основания ожидать появления разрывов при суммировании ряда целиком. Всякому нематематику ясно, что "топологически" график суммы ряда сходится к ломаной линии:

Да, это неоднозначная функция от x, и значениям отвечает континуум значений ординаты. Но кто таки нам мешает слегка повернуть оси, чтобы добиться полной однозначности? Геометрические формы не зависят от способа арифметизации. Кривая (траектория) остается все тем же геометрическим местом точек, как ее ни параметризуй: меняются представления объектов, но не сами объекты. Обратное тоже верно: одни и те же числовые структуры представляются разными объектами (в обыденной жизни — далекими от всякой математики). Всякое представление условно, частично, справедливо лишь в каком-то приближении (в контексте). Но какое-то представление всегда возможно и практически необходимо.

Кстати, трюк с малым смещением осей не нов: например, в теории функций комплексного переменного мы давно и привычно обходим таким способом полюса. Так чего нам стесняться в теории рядов Фурье?

Важно здесь, что ряд Фурье для всякой "приличной" функции f(x) сходится всегда к некоторой непрерывной (разумеется, периодической) функции F(x), которая, вообще говоря, не обязана совпадать с f(x). Чтобы устранить формальную неоднозначность можно попытаться перейти к параметрической записи функции — например, выбрав в качестве аргумента длину дуги:

Никаких разрывов при суммировании ряда Фурье в таком представлении, вроде бы, вообще не возникает, и "заполнение" кажущихся скачков получается само собой. Однако избавиться от проблем не удается: при увеличении числа членов ряда сумма сильно осциллирует (хотя и с убывающим размахом) — так что с предельным переходом опять не все просто; если исходно проблемы возникали только на концах отрезка, теперь неопределенность типа надо раскрывать в каждой внутренней точке. Для отделения тренда от вариаций существует стандартный трюк: мы "сглаживаем" кривую, убирая слишком быстрые осцилляции:

Колебания с периодами много меньшими Δx благополучно усредняются в ноль, и мы имеем дело с "хорошей", гладкой линией. С увеличением числа членов ряда усредненная функция стремится к тому же пределу F(x) — без всяких неопределенностей. Иногда, впрочем, именно отклонения от среднего представляют главный интерес. Один из практически важных примеров — теория музыки.

Совершенно аналогично обстоит дело с теоремой Дирихле. Например, из графика для частичной суммы ряда Фурье функции sgn(x)

мы снова усматриваем сходимость к ломаной линии, так что разрыв исходной функции заполняется при полном суммировании ряда вертикальным отрезком оси ординат, и вместо единичной разрывной ступеньки получается непрерывный меандр. И это правильно, поскольку всякая сумма периодических функций с соизмеримыми периодами есть функция периодическая, чего мы и ждем, интуитивно противопоставляя прямую и круг, качественно разные формы движения. Графики периодических функций — просто развертка круга (или многих кругов) вдоль прямой.

Несмотря на формальную сходимость тригонометрического ряда внутри ограниченного интервала, нельзя утверждать, что сходится он именно к той функции, по которой вычислены его коэффициенты. Тонкое строение иерархии (снимающее детали поведения частичных сумм) никуда не денется; и вычислять исходную функцию путем суммирования соответствующего ряда Фурье далеко не всегда целесообразно. И дело тут вовсе не в медленной сходимости, и не в особенностях поведения на краях. Любая наука говорит о чем-то вне нас (хотя бы мы в этом и участвовали как материальные обстоятельства и условия), и строение науки должно отвечать строению предмета. Там, где сама деятельность диктует применение Фурье-анализа, мы обязаны его использовать, как бы ни хотелось нам упростить себе жизнь выделением основных трендов, глобальных характеристик — вместо вроде бы малосущественных вариаций. Например, если прямая или ступенька получается в результате работы радиоэлектронных устройств, волновая природа процесса так или иначе проявится на практике — и тригонометрические ряды здесь в порядке вещей. Когда же мы говорим, допустим, о технологическом процессе, выгорании водорода в звезде или обычном киносеансе — естественнее линейное приближение (хотя бы и учетом возможных рефлексивных цепочек). Противоположности не существуют друг без друга, и наше дело — всему искать свое место.

Сухой остаток: понятие предела (в том числе предела ряда или интеграла) не так тривиально, как может показаться из школьного курса математического анализа. Сходится не число к числу — а объект к объекту (числа — частный случай). Функция может быть арифметизована ("вычислена") очень по-разному — ни одна из таких частных арифметизаций не выражает идею функции как таковой. Наши примеры "топологической" (или "экстенсиональной") сходимости никоим образом не исчерпывают всех возможностей. Они лишь подчеркивают отличие операционального определения функции от ее экстенсионала ("графика"). Но есть сколько угодно других форм определения (например, неявные, схематические, иллюстративные, прикладные), не сводящихся ни к операциям, ни к множествам. Иерархия всех возможных определенностей и есть функция в собственном смысле слова.

Понятно, что пересмотр понятия предела повлечет за собой соответствующие поправки в теорию дифференциала и интеграла. Особых потрясений для математики, разумеется, ожидать не приходится — но пробежаться по замшелости свежим взглядом иногда полезно.

Чисто практически, идея графического предела оказывается полезна там, где традиционная теория констатирует отсутствие предела и призывает доопределить нечто произвольным образом. А никакого произвола на самом деле нет, и кажущееся отсутствие сходимости связано лишь с неудачной параметризацией. Можно выдвинуть неформальный тезис, что все известные "экзотические" функции суть примеры неправильной (неестественной) арифметизации. При более осмысленном выборе описания, экзотика благополучно снимется, и все опять вернется к сочетанию простейших движений: прямой и круга — поступательности и рефлексии.