Equilibrium in Manifolds
General relativity theory is indeed one of the greatest breakthroughs in human reflection. Despite all its inherent fallacies, it gave us an entirely new perspective: nonlinearity. While the preceding centuries favored a linear, or at least linearized, picture of motion, admitting nonlinear effects as minor corrections or a statistical artefact, general relativity postulates nonlinear equations of motion, and there is no way to eliminate this principal self-reference from the physical science. A few decades later, nonlinear fields have become commonplace in fundamental theories, and the very kinematic layout is now to include all kinds of structural rearrangement.
With all that, the emancipation of nonlinearity lacks ideological guidance, hence looking quite arbitrary; no wonder that the most attractive results of nonlinear dynamics are mainly related to (quasi)stochastic behavior and chaos. Still, this brings yet another important premise: the geometry of physical motion does not need to follow the geometry of the underlying equations of motion; that is, the global structure of the ensemble of "world lines" is not necessarily a space (characterized with its overall dimensionality and topology), but rather a manifold "embedded" in a space structured according to the specific nature of the interactions involved. The next logical step is to limit the ubiquity of physics, allowing for changes in the equations of motion in the course of motion. In this way, two observers may also differ in their attitude to dynamical laws, and not merely the way of their parametrization, which demands yet another generalization of the notion of a frame of reference. In other words, there is no "embedding space" at all, and all we have is a physical manifold, with dynamically changing geometry.
An approach like that may seem too hard to develop. In a way, it undermines the foundations of physics as an "exact" science, putting it in the same row with the speculative disciplines like philology or sociology. On the other hand, such a comparison may be very productive, introducing physical notions of an entirely new character and stimulating the search for the corresponding experimental techniques, for mutual benefit.
Still, as long as we avoid too pretentious claims, certain aspects of manifold dynamics can be comprehended within the existing physical theories, with minor modifications. For instance, admit that the local dimensionality of motion may vary from one point to another, just like any other physical quantity. For a while, we do not consider abrupt changes (similar to "bifurcations"):
Here, there is a "critical" point, such as the manifold is one-dimensional on its left, and two-dimensional on the right. Such effects can be introduced later either through singular potentials or as quantum transitions. So far, let the dimension of the manifold change continuously:
Physically, there is no momentary transition, but rather a smooth migration from one to two dimensions in some physically (but never infinitely) small active area (denoted with the circle in the picture). Within this area, the dimension of the manifold can be represented by a real number. Today, in the era of fractals and dimensional renormalization, we are generally accustomed to (at least formally) non-integer dimensionalities, and this continuality does not evoke any objections. Now, to describe, say, relativistic motion, we can account for varying dimensionality in a straightforward manner, slightly modifying the traditional expression for the (invariant) interval:
The dimensionality of motion (as opposed to the dimension of space) is described with the parameter ν, and we need some "fundamental length"  to bring the dimension term to the units of length. Right here, there is already much to discuss. Thus, the sign of the dimensional term may hint to two opposite branches of physics that might be selectable by the appropriate asymptotic conditions. In this model, such "negative" and "positive" areas are utterly incompatible, which does not forbid their interaction via an additional level of hierarchy, or a quantum correlation. The correct choice of the sign for our branch of reality is a matter of thorough experimenting.
Note, that, for the negative branch, the sign of ds2 can negative for very small displacements (dx ~ 0, dt ~ 0); this might be a serious argument in favor of the positive branch, but also, as an alternative, an indication of some additional restrictions on the form of "physical" trajectories within the negative branch, as compared to the positive branch, which makes their physics very different.
As one can easily see, with the negative sign, the form of the interval much resembles the historical Kaluza-Klein approach, the predecessor of the modern string theories. However, there is an important difference in interpretation: instead of an abstract space in the background of physical motion, I suggest a revision of the very notion of dimensionality, allowing for its changes in physical interactions. Today, "theories of everything" are already showing the signs of stagnation due to the same conceptual difficulty as in the early 5-dimensional extensions: too much arbitrariness. It's fine to have enough freedom in our theorization; however, an excess of redundancy brings in an ad hoc air that has never been thought of as a merit. With the dimensional interpretation of the "fifth dimension", we can retain certain useful results, while avoiding the deadlock questions as to their nature and origin. As we will see, this new "coordinate" is entirely different from space and time; moreover, its introduction will essentially change the structure of the spatial part of the interval.
In the positive branch, the dimensional term is "time-like", and we recollect the old idea of a multi-time formalism for a relativistic treatment of many-body problems. Indeed, in a system of N material points, the formal number of the degrees of freedom equals 4N: one time and four spatial coordinates for each particle. Depending on the way we impose the relativistic constraint, different theories will emerge; some of them may incorporate two or more time dimensions. However, here again, it is the difference in interpretation that matters. In the dimensional extension of the interval, the last term refers to a specific quality other than mere space-time organization, a new level of the same hierarchy. A few words about the levels of time can be found below; still, the far-fetched consequences of physical branching in the dimensional extension are to be examined elsewhere.
Personally, I suppose that every formal possibility is practically implementable. Otherwise, we just could not have fancied it. The world behaves with us exactly like we behave in the world. As soon as we learn new behaviors, we discover a different world.
To proceed, note that I do not use the "reduced" time x0 = ct, like in almost every other text on theoretical physics. Even with the units chosen to bring the speed of light to unity, the factor c is still implied in the equation for the interval, to distinguish time from space. When we establish a correspondence between two physical (or any other) quantities, this does not mean that these quantities are of the same nature; otherwise, the very search for correspondence would be out of question. The invariance of the interval (which, probably, needs to be reinterpreted in our case) is just a kind of physical constraint (justified by the practically established constancy of the speed of light). It has nothing to do with reducing space to time, or the other way round; conversely, one might say that this reduction is only possible under the condition of the invariance of the relativistic interval (in the presence of the constraint). As we add yet another term to the expression, the physical nature of this equation becomes evident. In principle, there may be more terms (just like "chemical potentials" enter the second law of thermodynamics), for the invariant quantity to incorporate contributions from many physical processes other than mere displacement; in particular, our simple model also invokes the changes in manifold dimension. Of course, the presence of a units-reduction factor does not make variations of dimension into a kind of distance.
For distances and durations much greater than , the last term is negligible, and we are comfortably back to the usual dimension-static relativism, treating the threshold of dimension change as an impenetrable singularity, similar to the "relativistic barrier" or the Schwarzschild sphere.
Now, we come to the principal question: why should one add the dimensionality change term as a quadratic expression similar to those for space and time? It seems quite probable, that the very idea of a distance should be adjusted to variable dimensions, transforming the geometrical invariants into something entirely different, which would give the ordinary interval in the limit  . The example of the formula for velocity addition is always at hand.
The first (trivial) answer is "why not?" This is a very crude model applicable to the inner regions of the active area far from its boundaries, and we can use it like any other, just to illustrate the possible lines of thought. It does not deny any generalizations, and even implies them. To provide a better justification, I need to make a brief lyrical digression into the origin of the variation principles constituting the basis of the modern theoretical physics.
In the beginning, when the human culture was yet syncretic, science did not much differ from art or philosophy, and in particular, the time for scientific specialization did not yet come. Physics, geometry, astronomy, psychology and physiology, geology and economy, subjectively dealt with the different manifestations of the same. The primary concern of this rudimentary science was about equilibrium. Largely depending on the freaks of nature, the humanity needed something solid to grasp. That is why the first ever scientific laws were essentially static, revealing stable structures in any motion. Numbers, geometrical shapes, celestial orbits etc. were the instances of the universal equilibrium; later philosophers took them for pure ideas built in any perception and hence determining the form of thought.
For my purpose, it is enough to indicate the practical importance of right proportion in material production and economy. Ancient architects had to adapt to the force of gravity; all kinds of levers were largely used to compensate for muscular insufficiency; any measurement at all relied on the relative stability of both the thing to measure and the instrument. The appearance of mathematics and logic was mainly an attempt to fix the forms of reflection in the same equilibrium manner, thus laying the foundation for any academic (well-balanced) science.
To find the balance, the guiding idea was to slightly shift a piece in the whole and see what happens; for stability, the system must tend to return to the original state. When the dissipative factors are small, it may take quite a while for the transitory processes to subside; in the limit of zero friction, the system will infinitely keep its motion, but it will do it in a regular way! This is a new kind of equilibrium, which can formally be attributed to the presence of some auxiliary terms responsible for the observed dispersion in the configuration space. In the early dynamic models, forces were introduced on that compensatory basis, to preserve (at least formally) the overall equilibrium of a system in motion. Today we use the same equilibrium considerations minimizing the value of the action functional along a bunch of similar trajectories. The very presence of such a stability obviously implies a number of symmetries (that is, the range of admissible variations).
Mathematically, an equilibrium point is characterized with zero first derivative; any deviations from the (local) minimum must average to zero, and it is only the second-order terms that may have any physical significance. In particular, for a physical space, the definition of distance must combine the squares of displacements; otherwise, the motion will not be stable enough to form any observable pattern. Of course, this does not deny the possibility of such "unphysical" events; however, to practically cope with them, we need yet another level of hierarchy, a new kind of stability as a basis for new physics.
For an extra hint, take the well-known phenomenon of diffusion, where the expected distance form the origin is proportional to the square root of time. Similarly, the standard Schrödinger equation is linear in time, which implies a mixture of the different levels of description; however practical, such "mixed" models are not entirely consistent, and we have to justify them as approximations of a more general theory.
That is why accounting for variable dimensionality will involve the squared deviation of dimension, on the same footing with all the rest. We speak about a physical equilibrium, with all the variation principle ideology kept intact. Just introduce a small fundamental length, and do anything as before. More complex equations might arise outside the active area, when the inner motion and outer asymptotic are considered in parallel; such multilevel physics is certainly possible, but I am not going to discuss it right now.
One could object, that the distances close to the fundamental length (where the variable dimensionality effects can be of importance) are anyway too small to allow classical description, and quantum effects must necessarily be considered on that scale. This is a logical confusion. Quantum physics is all about correlation. It does not depend on the spatial or temporal scale. Yes, we first observed quantum behavior in microscopic systems; today, we admit quantum correlation in outer space, for huge astrophysical bodies, nothing to say about the usual human-sized objects like lasers, or the presumed quantum communication devices. Conversely, classical physics does not much depend on the system's size; for instance, cascades in atomic and nuclear reactions are quite classical in nature, and there is absolutely no reason to deny the possibility of ("quasi")classical behavior for very short distances and times. As soon as we can stage an experiment of the classical type, we do not need any quanta at all.
By the way, one could consider any quantum physics as built over some classical model (which is commonly referred to as "quantization"). In particular, the symmetry of the theory (the form of the interval) is to be chosen before we can introduce a quantum configuration space. Any modification in this (classical) constraint will influence the form of the corresponding quantum theory. In particular, adding the dimension-dependent term will significantly modify both classical and quantum predictions.
Of course, this approach is utterly incompatible with philosophical relativism denying the very idea of the physical systems and their interactions; there were numerous suggestions to replacing the objective order by mere psychological correlation etc. This is an entirely ideological choice, which is outside any science at all; it can hardly be too productive in the physics of space and time.
With the dimensionally-enhanced expression for the interval, general relativity can be introduced in the standard manner, through variable metric, which, in this case may also depend on dimensionality. A meaningful discussion of this generalization should be based on a clearer understanding of the meaning of the Einsteinian theory, which still does not seem to receive an acceptable (and logically consistent) interpretation. In the rest, I stick to the simplest form of the interval, though the conclusions may as well apply to the general case.
In a manifold of variable dimensionality, one cannot directly relate the local dimension with the number of independent coordinates. Dimension as a physical value is to be related to a hierarchy of degrees of freedom, constraints and the structure of the "observer", as discussed elsewhere. The spatial displacement (or uncertainty) dx2 is primarily measured along some trajectory (a world line), and it may be differently unfolded into the sum of individual contributions; such specifications determine the possible frames of reference. For the transition from 1-dimensional to 2-dimensional area (like in the above pictures), one will possibly consider simple two-component objects, with the "up" component corresponding to the fully unfolded 2-dimensional state, and the "down" component referring to the folded, 1-dimensional spatiality. Normalized to unity, this "spinor" will represent all the intermediate states, with the dimensionality between 1 and 2. This means that the relativistic coupling of space and time will also take two different forms, and we must consider a combination of the both. Similarly, if we need to continue a 1-dimensional trajectory into a 3D region, we'll have to add more components accounting for the different modes of unfolding; for instance, a representation with 2×2 matrices is intuitively attractive, with each of the two indices referring to the unfolding of the corresponding dimension. In the degenerate case of constant dimensionality, one component equals 1, and we arrive to the common representation of a frame of reference by a coordinate system. Of course, there are other possible frames built from less trivial mathematical constructs; however, all such representations correspond to the same physical reality, which does not depend on the way we fancy it. As usual, both classical and quantum pictures are equally conceivable, as well as any their combinations. Obviously, physical laws will change their form from one component to another, and it is not too unlikely that certain interactions that we consider as different within the standard model refer to the same interaction on the different levels of dimensional hierarchy.
In my dimensional model, there is yet another hierarchy related to the nature of time. This temporal hierarchy does not directly correspond to the spatial hierarchy introduced above; rather, it develops in an "orthogonal" direction. In every frame of reference, there is a "physical" time correlated with the measures of distance. For layered distances, reference time is the same for any dimensionality. This could be considered as a physical condition ensuring the integrity of motion. However, such metric time is not enough to describe the system's dynamics. There are two other levels of time that could be referred to as "inner" and "outer" time.
Indeed, always remaining in the equilibrium zone (that is, assuming the applicability of the variation analysis), we find that the traditional expression for relativistic action
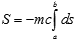
does not necessarily hold for the variable-dimension manifolds, since the "density" of trajectories may change with dimensionality (compare it to the functional of action in general relativity). Also, the initial and final point of the integration path may belong to the areas of different dimensionality, and there is no "inherent" ordering. We cannot, in general, speak of the interval as such, but rather about its local variations. Note that the factor mc is no longer convincing in the dimension-dependent case: first, the speed of light here plays a more modest role, along with the other "structural" constants, and second, the rest mass as a global (topological) characteristic of motion must certainly be replaced with a more flexible construct reducible to the constant mass in the regions of constant dimensionality. Still, as the manifold is deemed to be connected, there are physical trajectories between any two areas (on the global scale), so that one could proceed with an action functional taking a slightly modified form:
This assumes, first, an integration parameter that marks the physical stages in the transition from a to b; here, ρ(τ) represents the inner structure of the active area that cannot be entirely eliminated in any frame, and it is only in the limit of constant dimensionality (in the asymptotic region) that this density becomes constant (effectively eliminating the need for any additional time levels). As the structure of the integrand is related to the overall picture of interacting particles and fields, the integration parameter τ can easily be interpreted as a kind of upper-level time, imposed on the physical system by the apparatus setup; that is why I call it the "outer time". Each tick of this clock assumes an equilibrium state achieved after all the possible "probes" have already been damped (or averaged out). These transitory processes develop on a lower level folded in the physical (metric) point; when we speak of a variation, a small perturbation etc., we implicitly refer to that "inner" time.
The distinction between these three levels of hierarchy is relative: shifting the focus of attention up or down, we can make inner or outer time quite physical, while the former physical metric will give way to some other observables. For a far-fetched consequence, one might think of the relative nature of the distinctions between the interactions of the present standard model, as well as its partial reproduction on a different level, in a quite different context.
For a margin illustration, take the pitch levels in music. Each historically possible scale can be represented with a number of pitch zones, like in this picture for the common 12-zone scale:
The shaded areas correspond to the really perceptibly musical tones, while the possible (in this scale) deviations from the "exact" pitch belong to the level of inner time; the outer time will be associated with real intonation (sequences of notes and harmonies).
The interplay between the inner and outer levels is responsible for the observable mass spectrum. Indeed, consider a simple two-level mechanical system with the a relatively smooth motion on the higher level accompanied with very fast oscillations on the lower level. Physically, the inner motion will be represented in the expression for the interval (near the equilibrium) as an additional term proportional to its squared frequency; that is, as a kind of inner energy, and eventually a mass. This suggests a new line of thought in the theory of dimension-dependent metric: the changes in the manifold dimension could be related to its hierarchical structure, with the enhanced interval as above pertaining to the regions of restructuration (conversion of hierarchy). In this picture, the additional term for dimensional shift has much in common with Einstein's idea of geometry produced by matter and material motion modified by geometry. In a way, this approach might be considered as a formal alternative (or complement) to general relativity. While practically all the experimental evidence remain within the realm of post-Newtonian approximation, the observable effects (like the rotation of the orbit of Mercury) might as well be explained by a change in the dimensionality of the physical manifold; some physicists tried to intuitively account for this effect slightly modifying the inverse-square law for Coulomb force and gravity, which is not entirely consistent and hence the results were not quite satisfactory. The idea of metric dimensionality might also remove certain conceptual difficulties from the theory of very heavy attraction centers ("black holes") as well indicate the ways of bypassing the uncomfortable relativistic restrictions on the speed of physical interaction. In particular this may demand an explicit account for temporal hierarchies. In the simplest case, various multi-time forms for the interval are to introduce a hierarchy of "coupling constants". Eventually, the hierarchical picture will serve as a kind of generalized dimensionality on any physical manifold: a specific hierarchical structure is to be unfolded in each point, while any transition from one point to anther will require a restructuration, a conversion of the hierarchy.
And, once again, this is a new approach to the very nature of physical dynamics: instead of discussing the admissible structures in a space of a fixed dimensionality, we say that there is no pre-defined physical dimension, so that the dimension of any particular physical process is dynamically formed as a result of that very process, in some practical context, in the vicinity of a local equilibrium point. Space and time will no longer usurp the status of the a priori frame of any reflection at all; other ways of ordering the hierarchy of physical interactions may be possible under appropriate conditions, penetrating the other sciences as universal paradigms.
|
