Равновесие в многообразии
Общая теория относительности — несомненно, один из величайших прорывов в истории человеческой рефлексии. Несмотря на все свои логические проблемы, заслуга ОТО в том, что она решительно развернула наше мышление в сторону нелинейности. Предшествующие века предпочитали представлять движение линейно — или хотя бы в линеаризованной форме, — так что любые нелинейности рассматривались как не меняющие сути дела поправки, или чисто статистические артефакты. ОТО постулирует нелинейность на уровне уравнений движения — так что никакими техническими ухищрениями эту принципиальное самодействие из физики не устранить. Спустя десятилетия нелинейные взаимодействия прочно укоренились в теории поля, и уже на уровне кинематики приходится учитывать всевозможные структурные перестройки.
При всем при том, эмансипация нелинейности все еще далека от идейной определенности и потому выглядит чистейшим произволом. Не удивительно, что наиболее эффектные результаты нелинейной динамики в основном связаны с переходом к (квази)стохастичности и хаосу. Это по-своему полезно, поскольку подчеркивает возможность несовпадение наблюдаемой качественно геометрии движения с лежащими в его основе физическими симметриями. Другими словами, набор возможных "мировых линий" в общем случае уже не образует пространства (с присущими ему размерностью и топологией); скорее, это некое многообразие "вложенное" в пространство, заданное законами движения, природой физических взаимодействий. Однако напрашивается следующий логический ход: почему бы не отказаться от единообразия физики и не допустить изменение уравнений движения в процессе движения? Тогда два разных наблюдателя могут по-разному решать, что считать динамическими законами, — и дело не сводится к простому изменению параметризации. Устоявшиеся представления о системах отсчета потребуют очередного обобщения. Нет никакого "объемлющего пространства"; все, что нам дано, — физическое многообразие с динамически меняющейся геометрией.
Может показаться, что подобный подход на практике вряд ли осуществим. По большому счету, это размывает саму основу физики как "точной науки", ставит ее в один ряд с разного рода теоретическими спекуляциями, вроде филологии или социологии. С другой стороны, выявление каких-то точек соприкосновения может оказаться довольно продуктивным, требуя введения физических понятий нового типа и стимулируя развитие соответствующих экспериментальных методов, — которые окажутся полезными не только в физике.
Тем не менее, даже в рамках существующих физических теорий (с минимальными модификациями) возможно уяснить некоторые важные аспекты динамики многообразий. Пусть, скажем, локальная размерность движения может меняться от точки к точке — подобно любой другой физической величине. Пока оставим в стороне внезапные (скачкообразные) изменения типа "бифуркаций":
Здесь предполагается наличие "критической точки", такой, что многообразие одномерно слева от нее, но уже двумерно справа. Ничто не мешает ввести в теорию такого рода дискретность "задним числом", через сингулярность потенциалов или как квантовый переход. Пока допустим, что изменение размерности многообразия происходит непрерывно:
Физически, нет никакого единомоментного "расщепления"; вместо этого — постепенный переход от одномерного представления к двумерному в некоторой физически (но не бесконечно) малой активной области (обозначенной кружком на рисунке). Внутри этой области размерность многообразия можно представить вещественным числом. Мы давно живем в эпоху фракталов и размерной регуляризации — и уже приучены к (хотя бы формально) нецелым размерностям; поэтому такая непрерывность вряд ли вызовет у кого-то внутренний протест. Если, например, нам нужно описать релятивистское движение частицы, мы просто включаем в традиционное выражение для (инвариантного) интервала дополнительный член, учитывающий изменение размерности:
Здесь размерность движения (в отличие от размерности пространства) представлена (числовым) параметром ν; чтобы привести к единообразию единицы измерения, требуется введение некоторой "фундаментальной длины"  . Уже на этом этапе возникаем немало интересных вопросов для обсуждения. Так, два варианта знака перед вкладом от изменения размерности можно интерпретировать как возможность (и сосуществование) двух противоположных ветвей физики; выбор определенной ветви зависит от наложенных асимптотических условий. На этом уровне "положительная" и "отрицательная" ветви никак не соотносятся друг с другом — что никак не отменяет их связи через какой-то дополнительный уровень иерархии, или в форме квантовых корреляций. Тогда вопрос о знаке в той ветви, где мы сейчас находимся, можно решать в экспериментальном плане.
Заметим, что в отрицательной ветви знак ds2 может стать отрицательным при достаточно малых смещениях в пространстве и времени (dx ~ 0, dt ~ 0); это может послужить серьезным аргументом в пользу выбора положительного знака перед вкладом размерности — однако может оказаться, что речь идет лишь о дополнительных ограничениях на движение системы, а присутствие таких связей в отрицательной ветви придает ее физике характерные особенности, которые вполне могут оказаться наблюдаемыми.
Легко видеть, что выбор отрицательного знака приводит к конструкции во многом напоминающей ранние теории типа Калуцы-Кляйна, предшествовавшие современным струнным построениям. Однако интерпретация такого расширенного интервала здесь совершенно иная: вместо отнесения физических процессов к некоему абстрактному пространству фиксированной размерности — предлагается пересмотреть само понятие размерности, учитывая ее изменения в результате физических взаимодействий. Уже сейчас при взгляде на многомерные "теории всего" нас не покидает предчувствие застоя — по той же причине, по которой нас не устраивали ранние пятимерные конструкты: слишком много произвола. Когда в теории есть воздух, возможность тонкой настройки, — это хорошо; когда же такой избыточности перебор — подстройка превращается в подгонку, а строгая наука — в теоретизирование ad hoc. При размерной интерпретации "пятого измерения", можно было бы сохранить какие-то полезные результаты — избегая при этом тупиковых размышлений об их природе и происхождении. Как мы в дальнейшем увидим, размерность — "координата" другого типа, непохожая на время и пространство; более того, при этом расширяются и наши представления о строении пространственного блока в выражении для интервала.
В положительной ветви слагаемое размерности становится "времениподобным", и на ум приходят старые идеи вроде многовременного формализма для релятивистской постановки проблемы многих тел. Действительно, в системе N материальных точек исходное количество степеней свободы формально равняется 4N: одна временная и три пространственных координаты на каждую частицу. В зависимости от того, как мы накладываем релятивистские связи, получаются разные теоретические модели; некоторые из них вполне могут использовать несколько временных координат. Но и здесь следует отметить отличие размерного расширения от простого добавления временных координат: речь идет о принципиально ином качестве, другом уровне той же иерархии. Ниже приводятся какие-то соображения об иерархии времени, однако серьезное изучение далеко идущих последствий ветвления физики при размерном расширении интервала требует особого трактата.
Лично я полагаю, что любая формальная возможность практически реализуема. Иначе мы просто не смогли бы об этом подумать. Мир ведет себя при нас так, как мы ведем себя в нем. Осваивая новые деятельности, мы открываем другие миры.
Прежде чем переходить к дальнейшему, подчеркну сознательный отказ от использования "приведенного" времени x0 = ct, как его вводят в практически всех других текстах по теоретической физике. Даже если выбрать единицы измерения таким образом, что величина скорости света окажется численно равной единице, множитель c все равно подразумевается в выражении для интервала, поскольку он призван отличить время от пространства. Когда мы устанавливаем соответствие между разными физическими (или иными) величинами, это вовсе не означает, что эти величины одной природы; в противном случае, зачем бы нам устанавливать соответствие? Инвариантность интервала (которую в нашем случае придется, скорее всего, как-то переопределять) — всего лишь род физической связи, наложение которой оправданно в силу практически установленного постоянства скорости света. Это не имеет ничего общего со сведением пространства к времени, или наоборот. Напротив, говорить о формальной допустимости подобного сведения возможно лишь при условии инвариантности релятивистского интервала (то есть, когда на систему наложена соответствующая связь). Поскольку мы добавляем дополнительные слагаемые в выражение для интервала, физическая его природа становится совершенно очевидной. Ясно, что при необходимости возможно ввести еще какие-то члены — подобно тому, как второй закон термодинамики расширяемся за счет многочисленных "химических потенциалов". Инвариант теории будет, таким образом, учитывать вклады самых разных физических процессов, а не одного лишь перемещения. Частный случай — учет изменения размерности, как в нашей простой модели. Понятно, что необходимость приведения к единицам длины никак не делает размерность чем-то вроде расстояния.
Для смещений, много больших , последний член пренебрежимо мал, и мы сразу же оказываемся в области применимости обычной теории относительности, в пространствах постоянной размерности, в которых точка перехода от одной размерности к другой выглядит непреодолимой сингулярностью, вроде сферы Шварцшильда или "релятивистского барьера".
Тут есть и принципиальный вопрос: а почему, собственно, мы имеем право вводить поправку на изменение размерности в виде квадратичного слагаемого, подобно временной и пространственной компонентам? Вполне может оказаться, что в пространствах переменной размерности следует изменить само понятие расстояния, и сугубо геометрические инварианты превратятся в нечто совершенно иное, что сводится к обычному интервалу только в пределе  . Сразу вспоминается пример с законом сложения скоростей...
Первый (тривиальный) ответ: а почему бы и нет? Это весьма грубая модель, применимая лишь вдали от границ активной области; и она ничем не хуже другой может проиллюстрировать возможные направления мысли. Она не только не отметает дальнейших обобщений — но даже предполагает их. Более глубокое обоснование потребует небольшого лирического отступления: обратимся к происхождению вариационных принципов, на которых зиждется вся современная теоретическая физика.
В самом начале, когда человеческая культура во многом была синкретична, наука не особенно отличалась от искусства или философии; в частности, эпоха научной специализации еще была далеко впереди: физика, геометрия, астрономия, психология и физиология, геология или экономика, — все это лишь разные проявления одного и того же. Главная цель этой рудиментарной науки — поиск равновесия. Слишком подверженное капризам природы, человечество нуждалось в хоть какой-то почве под ногами. Поэтому первые научные законы оказывались по преимуществу статичными: они говорили о постоянном в любом движении. Числа, геометрические фигуры, орбиты небесных тел и т. д. — это примеры универсального равновесия. Некоторые философы последующих веков просто объявляли их чистыми идеями, априорными формами всякого восприятия — и следовательно, единственно возможными формами мысли.
Но здесь мне достаточно отметить практическую важность правильных пропорций в материальном производстве и в экономике. Античным архитекторам приходилось мириться с силой гравитации; всевозможные рычаги позволяли преодолеть недостаточность мышечного усилия; всякое измерение в конечном итоге опиралось на предположение об относительной неизменности как измеряемого, так и инструмента. Установление норм математического и логического рассуждения лежит в том же русле: это попытка зафиксировать столь же равновесные формы мышления — и тем самым заложить основы академической (правильно сбалансированной) науки.
На практике поиск равновесия сводился, главным образом, к тому, чтобы слегка пошевелить конструкцию — и посмотреть, что случится; всякая устойчивая система должна так или иначе вернуться в исходное состояние. Если диссипативные факторы малы, это возвращение может потребовать немалого времени, а в пределе нулевого трения система вообще никогда не успокоится — но это движение все-таки будет по-своему регулярным! Это иное, расширенное представление о равновесии, которое формально проистекает из присутствия неких добавочных (компенсаторных) сил, отвечающих за наблюдаемые отклонения от равновесной конфигурации. Именно так определялись силы в ранних динамических теориях: только с учетом такой компенсации удавалось (хотя бы формально) восстановить общий баланс. В наши дни эти соображения стандартизированы — и равновесие мы ищем, минимизируя значение функционала действия на пучках сравнительно близких траекторий. Понятно, что само наличие равновесия подразумевает какие-то симметрии (то есть, зону допустимых вариаций).
Математически, в точке (локального) равновесия первая производная обращается в ноль; в статистическом плане, в ноль обращается среднее отклонение от равновесия. Таким образом, только члены второго порядка малости могут иметь физический смысл. В частности, определение расстояния в физическом пространстве должно как-то комбинировать именно квадраты смещений; иначе поведение системы не будет достаточно устойчивым, чтобы наблюдалось нечто вполне определенное. Разумеется, это не означает полной невозможности таких "нефизических" движений — но для их наблюдения и практического освоения придется задействовать какой-то иной уровень иерархии, и найти для этой новой физики более общее понятие равновесности.
В качестве полезной параллели — всем знакомое явление диффузии, где ожидаемое удаление от источника пропорционально квадратному корню времени. Аналогично, стандартное уравнение Шредингера линейно по времени — это явное смешение разных уровней описания; несмотря на удобство и практичность, таким теориям недостает внутренней последовательности, и мы вынуждены обосновывать их, выводя как частные случаи более общей схемы.
Исходя из этого, минимальное введение переменной размерности будет опираться на квадрат отклонения, наряду с квадратами всех прочих отклонений. Так мы остаемся в рамках все той же равновесной физики, сохраняем ее вариационный принцип. Достаточно слегка подправить "лагранжиан" — и действовать в привычной манере. Конечно, при выходе за границы активной области могут потребоваться более сложные методы, поскольку внутреннее движение и асимптотическое поведение рассматриваются на равных правах. Однако от обсуждения таких ситуаций я на данный момент воздерживаюсь.
Могут возразить, что смещения порядка фундаментальной длины (при которых начинают играть эффекты изменения размерности) в любом случае слишком малы, чтобы опираться на классическую механику, и надо в обязательном порядке использовать квантовые технологии. Однако это чисто логическая путаница. Квантовая механика ничего не говорит о характерных расстояниях и временах — она занимается исключительно корреляциями. Да, исторически квантовое поведение наблюдалось в микроскопических (по сравнению с нами) системах; однако сегодня мы допускаем квантовые корреляции даже в космосе, для огромных астрофизических объектов, — что уж говорить о бытовых вещах, вроде лазеров или будущих устройств квантовой связи. Со своей стороны, классическая физика никак не опирается на размеры систем. Например, каскады в атомных и ядерных реакциях вполне классичны по природе. Аналогично, нет совершенно никаких оснований отрицать возможность (квази)классического поведения для очень коротких промежутков пространства и времени. Достаточно организовать эксперимент так, чтобы на выходе получать нечто классическое — и никакие кванты нам тогда не нужны.
В конце концов, квантовая физика как таковая представляется своего рода надстройкой над определенной классической моделью (и для этого есть старинный термин: "квантование"). В частности, нам приходится выбирать симметрию теории (строение интервала) прежде чем мы сможем осмысленно говорить о квантовом конфигурационном пространстве. Всякое изменение этой (классической) связи влечет за собой перестройку соответствующей квантовой теории. Соответственно, введение плавающей размерности существенно изменит и классические, и квантовые результаты.
Конечно же, здесь ничего общего с философским релятивизмом, отрицающим само существование физических систем и взаимодействий между ними. Буржуазные философы много раз пытались подменить объективный порядок вещей сугубо психологическими корреляциями или чем-то в этом роде. Это их идеологический выбор, который изначально вне науки; подобные взгляды вряд ли помогут осмысленно обсуждать физику пространства и времени.
Для расширенного размерными вкладами интервала возможны обобщения в духе общей теории относительности, с локальными метриками, зависящими от пяти параметров. Сколько-нибудь осмысленно обсуждать такие построения возможно только на базе четких представлений о смысле эйнштейновской теории — которая до сих пор не получила приемлемой (и логически последовательной) интерпретации. Ниже я предполагаю ограничиться обсуждением простейших интервалов, — хотя какие-то выводы могут быть справедливы и для общего случая.
На многообразии переменной размерности у нас уже нет возможности напрямую связать локальную размерность с количеством независимых координат. Размерность как физическое понятие представляется иерархией степеней свободы, связей и структур "наблюдателя" — как указано в другой статье. Пространственное смещение (или неопределенность) dx2 предполагает, главным образом, измерение вдоль некоторой траектории (мировой линии); эту величину можно по-разному представлять в виде суммы качественно разных слагаемых — и каждое такое представление задает некоторую систему отсчета. Например, для перехода от одномерного в двумерному движению (как на рисунке выше) мы могли бы ввести простые двухкомпонентные объекты — столбцы, в которых "верхняя" компонента относится к полностью развернутому двумерному пространству, а "нижняя" описывает свернутое, одномерное состояние. Если этот "спинор" нормализовать на единицу, мы можем учесть все промежуточные ситуации, когда размерность лежит между единицей и двойкой. А значит, и релятивистское связывание пространства и времени способно принимать две параллельных формы, и придется строить их комбинацию. Точно так же, при развертывании одномерного движения в трехмерное нужны добавочные компоненты, отвечающие за различные направления развертывания. Например, интуитивно привлекательно представление матрицами 2×2, где каждый индекс отвечает за развертывание соответствующего пространственного измерения. В вырожденном случае, когда размерность движения постоянна, одна из компонент равна 1, а остальные обращаются в ноль; мы возвращаемся к обычному координатному представлению системы отсчета. Разумеется, возможны и нетривиальные системы отсчета, представленные сложными математическими конструктами. Тем не менее, все такие представления отвечают одной и той же физической реальности, которая никак не зависит от того, что мы о ней думаем. Здесь также допустимо как классическое, так и квантовое описание — или их комбинация. Форма физических законов, конечно же, будет различной для компонент разного типа; вполне может оказаться, что какие-то из элементов нынешней стандартной модели говорят об одном и том же на разных уровнях.
В модели с переменной размерностью полезно помнить о еще одной иерархии, связанной с природой времени. Эта временная иерархия не повторяет описанное выше развертывание пространственных координат, а наоборот, скорее "ортогональна" ему. В каждой системе отсчета имеется "физическое" время, соотносимое с пространственными измерениями. При наличии размерного вклада пространственные координаты представлены иерархическими структурами, однако время системы отсчета одинаково для всех компонент. Это физическое условие, обеспечивающее целостность движения. Но для описания динамики недостаточно одного лишь "метрического" времени. Есть еще два уровня времени, которые можно было бы назвать "внутренним" и "внешним" временем.
В самом деле, даже целиком оставаясь в пределах зоны равновесия (где применимость вариационного анализа не вызывает сомнений), мы можем обнаружить, что традиционное выражение для релятивистского действия
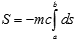
не всегда применимо к многообразиям переменной размерности, поскольку "плотность" траекторий может меняться в зависимости от текущей физической размерности (ср. логику построения функционала действия в ОТО). Поскольку же начальная и конечная точка траектории могут лежать в пространствах разной размерности, здесь нет "естественного" упорядочения. Как и во многих других случаях, мы не можем говорить об интервале вообще — но только лишь о приращениях интервала, о локальных отклонениях. К тому же множитель mc перед интегралом в условиях переменной размерности выглядит уж очень неубедительно: скорость света играет здесь отнюдь не ведущую роль, это лишь одна из "структурных" констант; с другой стороны, массу покоя как глобальную (топологическую) характеристику движения придется заменить чем-то более гибким, что сводится к постоянной массе в областях, где размерность движения не меняется. Тем не менее, поскольку мы рассматриваем связные многообразия, существуют физические траектории между любыми его областями, глобально. Поэтому действие все еще возможно записать в (несколько измененном) интегральном виде:
Прежде всего, это предполагает, что переменная интегрирования может играть роль времени, перечисляя физически значимые промежуточные этапы при переходе от a к b; при этом ρ(τ) характеризует внутреннюю организацию активной области, которая не может быть устранена ни в какой системе отсчета — и только асимптотически, в пределе постоянной размерности вырождается в константу (и тогда дополнительные уровни времени просто не нужны). Поскольку структура подынтегрального выражения связана с общей картиной взаимодействия частиц и полей, переменная интегрирования τ представляет время на более высоком уровне, где на физическую систему накладываются связи со стороны аппаратного комплекса; поэтому оно и называется внешним временем. Каждое его мгновение предполагает равновесное состояние, к которому система приходит после диссипации (или усреднения) влияния любых пробных тел. Связанные с ними переходные процессы свернуты в каждой точке физического (метрического) уровня — но когда мы говорим о вариациях, о малых возмущениях и т. п., мы неявно ссылаемся на это, внутренне время.
Различие между этими тремя уровнями относительно: сдвигая фокус внимания по этой иерархической структуре вверх или вниз, мы можем вытащить в физическую область внутреннее или внешнее время, а прежние наблюдаемые (параметры системы отсчета) уступят место другим способам описания. В качестве фантастического предположения, можно задуматься об относительности различения взаимодействий нынешней стандартной модели — а также о возможности ее частичного воспроизведения на другом уровне, в совершенно ином контексте.
В качестве иллюстрации на полях, обратимся к уровням звуковысотности в музыке. Каждая исторически возможная звуковысотная система может быть представлена набором зон, подобно показанным на этом графике для обычного 12-ступенного звукоряда:
Заштрихованные области отвечают реально воспринимаемым музыкальным тонам, а возможные (в пределах зоны) отклонения от "точной" высоты принадлежат уровню внутреннего времени. Внешнее время соотносится здесь с реальными интонациями (последовательностями нот или гармониями).
Соотношением внутреннего и внешнего времени определяется наблюдаемый спектр масс. В самом деле, возьмите простую двухуровневую механическую систему, в которой движение на верхнем уровне происходит сравнительно гладко, а на нижнем уровне имеются очень быстрые осцилляции. Физически, внутреннее движение будет представлено в выражении для интервала (недалеко от точки равновесия) дополнительным членом, пропорциональным квадрату частоты, как вклад внутренней энергии, и в конечном итоге как дополнительная масса. Отсюда еще одно направление развития метрической модели размерности: изменения размерности многообразия связаны в перестройкой его иерархической структуры (обращением иерархии). Тогда появление дополнительных вкладов в интервал в зоне перестройки принципиально не отличается от эйнштейновской идеи: движение материи порождает геометрию, а геометрия влияет на движение материи. Учет переменной размерности можно тогда рассматривать в качестве альтернативы (или дополнения) общей теории относительности. Пока практически все экспериментальные подтверждения не выходят за рамки пост-ньютоновского приближения, наблюдаемые эффекты (вроде поворота орбиты Меркурия) с тем же успехом можно было бы интерпретировать в духе переменной размерности физического многообразия. Попытки слегка подправить кулоновские силы и ньютоновскую гравитацию путем изменения показателя степени лежат в том русле — но это чисто феноменологический подход, который не может привести к сколько-нибудь последовательной теории. Техника метрической размерности может быть полезна для устранения ряда концептуальных трудностей — например в теории сверхмассивных центров притяжения ("черных дыр"), — а также в связи с поиском способов преодоления релятивистских ограничений на скорости распространения взаимодействий. В частности, здесь потребуются модели с явным учетом иерархичности времени. В простейшем случае это приведет к выражениям для интервала с несколькими временными вкладами — и разными "константами связи". В конечном итоге, иерархичность станет своего рода обобщением понятия размерности на случае произвольных физических многообразий: в каждой точке развертывается некая физическая иерархия — а переход от точки к точки сопровождается обращением иерархии.
И в завершение хотелось бы еще раз отметить главную особенность размерной динамики: вместо исследования динамически возникающих структур в пространстве фиксированной размерности мы переходим к рассмотрению динамически возникающей размерности, выражающей строение физической системы вблизи некоторой локальной точки равновесия — в конечно итоге это связано с контекстом человеческой деятельности. Время и пространство больше не могут играть роль априорных предпосылок всякой рефлексии: в определенных условиях возможны иные способы развертывания иерархии физических взаимодействий, и это неизбежно приведет к появлению тех же парадигм в других науках.
|
